题目内容
13.菱形ABCD,∠ABC=60°,BD=6$\sqrt{3}$,点E在AB上,CE=2$\sqrt{7}$,将CE绕点C旋转60°得到线段CF交BD于F,则DF的长为2或4.分析 先证明△ABC、△ACD是等边三角形,得出AC=AB=CD=AD,由三角函数求出AB,再证明△BCE≌△ACF,得出CE=CF=2$\sqrt{7}$,作FG⊥CD于G,设DG=x,则DF=2x,FG=$\sqrt{3}$x,CG=6-x,根据勾股定理得出方程(6-x)2+($\sqrt{3}$x)2=(2$\sqrt{7}$)2,解方程得出x,即可得出DF.
解答 解:连接AC,如图所示: ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD=$\frac{1}{2}$BD=3$\sqrt{3}$,AB=BC=CD=DA,
∵∠ABC=60°,
∴△ABC、△ACD是等边三角形,
∴AC=AB=CD=AD,∠ACB=∠CAD=∠ACD=60°,
∴AB=$\frac{OB}{sin60°}$=$\frac{3\sqrt{3}}{\frac{\sqrt{3}}{2}}$=6,
∴CD=AB=6,
∵∠ECF=60°,
∴∠BCE=∠ACF,
在△BCE和△ACF中,$\left\{\begin{array}{l}{∠EBC=∠FAC=60°}&{\;}\\{BC=AC}&{\;}\\{∠BCE=∠ACF}&{\;}\end{array}\right.$,
∴△BCE≌△ACF(ASA),
∴CE=CF=2$\sqrt{7}$,
作FG⊥CD于G,设DG=x,则DF=2x,FG=$\sqrt{3}$x,CG=6-x,
根据勾股定理得:CG2+FG2=CF2,
即(6-x)2+($\sqrt{3}$x)2=(2$\sqrt{7}$)2,
解得:x=1或2,
∴2x=2或4,即DF=2或4.
点评 本题考查了菱形的性质、旋转的性质、全等三角形的判定与性质、等边三角形的判定与性质以及三角函数;通过作辅助线证明全等三角形和等边三角形是解决问题的关键.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案

 如图,已知BD为∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,CD与BD交于点D,试说明∠A=2∠D.
如图,已知BD为∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,CD与BD交于点D,试说明∠A=2∠D.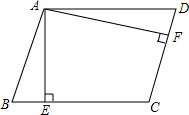 如图所示,?ABCD的相邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=4cm,求AF的长.
如图所示,?ABCD的相邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=4cm,求AF的长. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是3,S3的值为$\frac{81}{8}$.
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是3,S3的值为$\frac{81}{8}$.