题目内容
8. 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.(1)求证:∠DAN=90°;
(2)求证:四边形ADCE是一个矩形;
(3)当△ABC满足什么条件时,四边形ADCE是一个正方形?请给出证明;
当四边形ADCE是正方形,若AB=3$\sqrt{2}$,求正方形ADCE的面积.
分析 (1)利用角平分线的定义和邻补角的定义即可得出∠DAN的度数;
(2)利用有三个内角是直角的四边形是矩形的判断方法即可;
(3)利用邻边相等的矩形是正方形,求出正方形的边长,从而求出正方形的面积.
解答 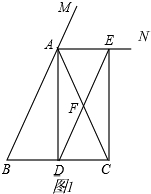
(1)证明:如图1,∵AB=AC,AD⊥BC,垂足为D,
∴∠CAD=$\frac{1}{2}∠$BAC.
∵AN是△ABC外角的平分线,
∴∠CAE=$\frac{1}{2}∠$CAM,
∵∠BAC与∠CAM是邻补角,
∴∠BAC+∠CAM=180°,
∴∠DAN=∠CAD+∠CAE=$\frac{1}{2}$(∠BAC+∠CAM)=90°,
(2)证明:∵AD⊥BC,CE⊥AN,∠DAN=90°,
∴∠ADC=∠CEA=∠DAN=90°,
∴四边形ADCE为矩形.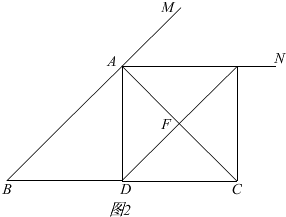
(3)解:如图2,当△ABC是等腰直角三角形时,四边形ADCE是一个正方形.
∵∠BAC=90°,且AB=AC,AD⊥BC,
∴∠CAD=$\frac{1}{2}∠$BAC=45°,
∠ADC=90°,
∴∠ACD=∠CAD=45°,
∴AD=AC.
∵四边形ADCE为矩形,
∴四边形ADCE为正方形.
由勾股定理,得$\sqrt{{AD}^{2}{+CD}^{2}}$=AC,
∵AD=CD,
∴$\sqrt{2}$AD=3$\sqrt{2}$,
∴AD=3,
∴正方形ADCE的面积=AD2=3×3=9.
点评 本题是四边形的综合题,主要考查正方形的判断方法,涉及到知识有,等腰三角形的三线合一的性质,如由AB=AC,AD⊥BC得到∠CAD=$\frac{1}{2}∠$BAC,三角形的外角的平分线,勾股定理;本题的关键是整体计算∠DAN=∠CAD+∠CAE=$\frac{1}{2}$(∠BAC+∠CAM)=90°.

练习册系列答案
相关题目
13.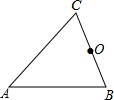 如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
 如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )
如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
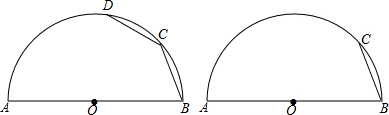
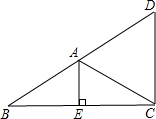 已知:如图AE⊥BC,∠EAC=∠ACD,试说明BC垂直于DC.
已知:如图AE⊥BC,∠EAC=∠ACD,试说明BC垂直于DC.