题目内容
1.解方程组或不等式组①$\left\{\begin{array}{l}{x+2y=10}\\{2x-3y=6}\end{array}\right.$;
②$\left\{\begin{array}{l}{x+1>3}\\{2+x≥2(x-1)}\end{array}\right.$.
分析 (1)①×-②得出7y=14,求出y,把y的值代入②求出x即可;
(2)先求出每个不等式的解集,再根据找不等式组解集的规律找出即可.
解答 解:①$\left\{\begin{array}{l}{x+2y=10①}\\{2x-3y=6②}\end{array}\right.$
①×2-②得:7y=14,
解得:y=2,
把y=2代入②得:2x-6=6,
解得:x=6,
所以原方程组的解为:$\left\{\begin{array}{l}{x=6}\\{y=2}\end{array}\right.$;
②$\left\{\begin{array}{l}{x+1>3①}\\{2+x≥2(x-1)②}\end{array}\right.$
∵解不等式①得:x>2,
解不等式②得:x≤4,
∴不等式组的解集是2<x≤4.
点评 本题考查了解一元一次不等式组和解二元一次方程组的应用,能把二元一次方程组转化成一元一次方程是解(1)的关键,能根据不等式的解集得出不等式组的解集是解(2)的关键.

练习册系列答案
相关题目
9.某商场用18万购进A、B两种电器,销售完共获利5万元,其进价和售价如表:
(1)该商场购进A、B两种电器各多少台?
(2)商场第二次以原价购进A、B两种电器,购进A电器的台数不变,B电器的台数是第一次的$\frac{1}{2}$;B种电器按原价出售,而A种电器打折销售.若两种电器销售完毕,要使第二次经营获利不少于25000元,A种电器最低售价为每台多少元?
| A | B | |
| 进价(元/台) | 500 | 600 |
| 售价(元/台) | 600 | 790 |
(2)商场第二次以原价购进A、B两种电器,购进A电器的台数不变,B电器的台数是第一次的$\frac{1}{2}$;B种电器按原价出售,而A种电器打折销售.若两种电器销售完毕,要使第二次经营获利不少于25000元,A种电器最低售价为每台多少元?
10.一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )
| A. | $\frac{8}{3}$ cm | B. | $\frac{16}{3}$ cm | C. | 3cm | D. | $\frac{4}{3}$ cm |
 如图,AC=AD,BC=BD,求证:△ABC≌△ABD.
如图,AC=AD,BC=BD,求证:△ABC≌△ABD.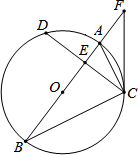 如图,在⊙O中,直径AB平分弦CD、AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
如图,在⊙O中,直径AB平分弦CD、AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B. 如图所示,在Rt△ABC中,∠B=90°,AC=100cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤25).过点D作DF⊥BC于点F,连接DE,EF.
如图所示,在Rt△ABC中,∠B=90°,AC=100cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤25).过点D作DF⊥BC于点F,连接DE,EF.