题目内容
4.某超市计划购进甲、乙两种品牌的新型节能灯20盏,这两种台灯的进价和售价如表所示:| 甲 | 乙 | |
| 进价(元/件) | 40 | 60 |
| 售价(元/件) | 60 | 100 |
(1)若购进两种台灯的总费用不超过1100元,那么超市如何进货才能获得最大利润?最大利润是多少?
(2)最终超市按照(1)中的方案进货,但实际销售中,由于乙品牌的台灯销售前景不容乐观,超市计划对乙品牌台灯进行降价销售,当每盏台灯最多降价多少元时,全部销售后才能使利润不低于550元.
分析 (1)利用甲、乙两种品牌售价与进价以及其数量得出w与x的函数关系式,再利用一次函数增减性得出答案;
(2)利用(1)中所求,进而得出降价后利润进而得出答案.
解答 解:(1)设获得的总利润为w元,
根据题意,得w=(60-40)x+(100-60)(20-x)=-20x+800,
又∵购进两种台灯的总费用不超过1100元,
∴40x+60(20-x)≤1100,
解得:x≥5,
∵在函数w=-20x+800中,w随x的增大而减少,
∴当x=5时,w取得最大值,最大值为700元,
故当甲种台灯购进5盏,乙种台灯购进15盏时,超市获得的利润最大,最大利润为700元.
(2)设每盏台灯降价m元,根据题意,
得700-15m≥550,
解得m≤10,
故当每盏台灯最多降价10元时,全部销售后才能使利润不低于550元.
点评 此题主要考查了一次函数的应用以及一次函数增减性和一元一次不等式的应用,正确得出w与x的函数关系式是解题关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
10. 如图,已知∠2=100°,要使AB∥CD,则须具备另一个条件( )
如图,已知∠2=100°,要使AB∥CD,则须具备另一个条件( )
 如图,已知∠2=100°,要使AB∥CD,则须具备另一个条件( )
如图,已知∠2=100°,要使AB∥CD,则须具备另一个条件( )| A. | ∠1=100° | B. | ∠3=80° | C. | ∠4=80° | D. | ∠4=100° |
 如图,有一块直角三角形纸片,AC=6,BC=8,现将△ABC沿直线AD折叠,使AC落在斜边AB上,且C与点E重合,则AD=3$\sqrt{5}$.
如图,有一块直角三角形纸片,AC=6,BC=8,现将△ABC沿直线AD折叠,使AC落在斜边AB上,且C与点E重合,则AD=3$\sqrt{5}$. 如图所示,AB∥CD,OE平分∠AOC,OE⊥OF,点O为垂足,∠C=50°,求∠AOF的度数.
如图所示,AB∥CD,OE平分∠AOC,OE⊥OF,点O为垂足,∠C=50°,求∠AOF的度数.
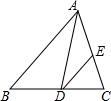 如图,已知AD是△ABC的角平分线,过点D作DE∥AB,交AC于点E,∠B=50°,∠ADE=30°,求∠C的度数.
如图,已知AD是△ABC的角平分线,过点D作DE∥AB,交AC于点E,∠B=50°,∠ADE=30°,求∠C的度数.