题目内容
18.已知四边形ABCD中,AB=6,CD=8,E、F分别是AD、BC的中点,则线段EF长的取值范围是( )| A. | 2<EF<14 | B. | 1<EF≤7 | C. | 6<EF<7 | D. | 2<EF<6 |
分析 首先设G是BD的中点,连接EG、FG,根据三角形的中位线定理,求出EG、FG的长度各是多少;然后在△EFG中,根据任意两边之和大于第三边三边,任意两边之差小于第三边,求出线段EF长的取值范围即可.
解答 解:如图1、图2,G是BD的中点,连接EG、FG,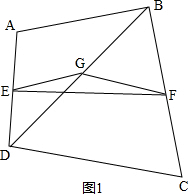 ,
,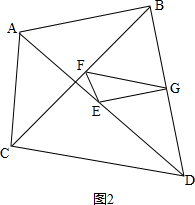 ,
,
∵E是AD的中点,G是BD的中点,
∴EG∥AB,且EG=$\frac{1}{2}AB$=$\frac{1}{2}×6=3$;
∵F是BC的中点,G是BD的中点,
∴FG∥CD,且FG=$\frac{1}{2}CD$=$\frac{1}{2}×8=4$;
∵FG-EG=4-3=1,FG+EG=4+3=7,
图1中,AB∥DC时,EF=7.
∴线段EF长的取值范围是:
1<EF≤7.
故选:B.
点评 (1)此题主要考查了三角形的中位线定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的中位线平行于第三边,并且等于第三边的一半.
(2)此题还考查了三角形的三条边的长度关系,要熟练掌握,解答此题的关键是要明确:任意两边之和大于第三边三边,任意两边之差小于第三边三边.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.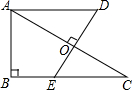 如图,在△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为( )
如图,在△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为( )
 如图,在△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为( )
如图,在△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=3,BC=4,则AD的长为( )| A. | $\frac{25}{4}$ | B. | $\frac{25}{8}$ | C. | $\frac{15}{4}$ | D. | $\frac{15}{8}$ |
9.某酒店客房有三人间、双人间客房,收费标准如下:
为吸引游客,实行团体入住五折优惠.一个40人的旅游团在优惠期间到该酒店入住,住了一些三人间普通和双人间普通客房.若每间客房正好住满,且一天共花去住宿费1220元,则旅游团住了三人间普通和双人间普通客房各多少间?
| 普通(元/间/天) | 豪华(元/间/天) | |
| 三人间 | 150 | 300 |
| 双人间 | 140 | 400 |
3.某班有50名同学,期末考试优秀的学生人数及科目如表:
这里,一科优秀者包括两、三科优秀者,两科优秀者里也包括三科优秀者,试说明上述统计表的错误.
| 单科 | 两科 | 三科 | |||||
| 科目 | 数学 | 英语 | 语文 | 语文 数学 | 英语 数学 | 英语 语文 | 语文、数学、英语 |
| 人数 | 32 | 31 | 29 | 16 | 17 | 18 | 10 |
7.下列计算正确的是( )
| A. | 2t-t=2 | B. | t2•t3=t6 | C. | (-t2)3=-t5 | D. | t3÷t2=t |
8.-$\frac{1}{3}$的绝对值为( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | 0 |
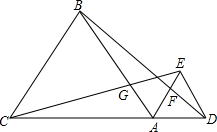 如图,A是CD上的一点,△ABC,△ADE都是正三角形,求证:(1)CE=BD;(2)CG=BF.
如图,A是CD上的一点,△ABC,△ADE都是正三角形,求证:(1)CE=BD;(2)CG=BF.