题目内容
11.已知关于x,y的方程组$\left\{\begin{array}{l}{2x+3y=4m+y}\\{x-y=3m-4}\end{array}\right.$,且它的解是x-8>y.(1)使用含m的式子表示方程组的解;
(2)求实数m的取值范围;
(3)化简|4-m|+|m+1|.
分析 (1)根据二元一次方程组的解法进行解答即可;
(2)根据它的解是x-8>y,列出不等式,即可解答;
(3)根据(2)中m的取值范围,即可解答.
解答 解:(1)方程组$\left\{\begin{array}{l}{2x+3y=4m+y}\\{x-y=3m-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{7}{4}m-1}\\{y=-\frac{5}{4}m+3}\end{array}\right.$;
(2)∵x-8>y,
∴$\frac{7}{4}m-1-8>-\frac{5}{4}m+3$,
解得:m>4.
(3)∵m>4,
∴4-m<0,m+1>0,
|4-m|+|m+1|=m-4+m+1=2m-3.
点评 本题考查了二元一次方程组、一元一次不等式、绝对值,解决本题的关键是求出二元一次方程组的解.

练习册系列答案
相关题目
3.某班有50名同学,期末考试优秀的学生人数及科目如表:
这里,一科优秀者包括两、三科优秀者,两科优秀者里也包括三科优秀者,试说明上述统计表的错误.
| 单科 | 两科 | 三科 | |||||
| 科目 | 数学 | 英语 | 语文 | 语文 数学 | 英语 数学 | 英语 语文 | 语文、数学、英语 |
| 人数 | 32 | 31 | 29 | 16 | 17 | 18 | 10 |
 正方形ABCD在坐标系中的位置如图所示,其中A(-1,2),将正方形ABCO绕O点顺时针旋转90°后,则B点旋转后的对应坐标为(3,-1).
正方形ABCD在坐标系中的位置如图所示,其中A(-1,2),将正方形ABCO绕O点顺时针旋转90°后,则B点旋转后的对应坐标为(3,-1).



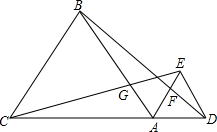 如图,A是CD上的一点,△ABC,△ADE都是正三角形,求证:(1)CE=BD;(2)CG=BF.
如图,A是CD上的一点,△ABC,△ADE都是正三角形,求证:(1)CE=BD;(2)CG=BF. 如图,抛物线与x轴交于A、B两点,与y轴交于C点,点A的坐标(2,0),点C的坐标为(0,3)它的对称轴是直线x=-1.
如图,抛物线与x轴交于A、B两点,与y轴交于C点,点A的坐标(2,0),点C的坐标为(0,3)它的对称轴是直线x=-1.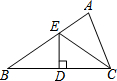 如图,在△ABC中,BC边的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )
如图,在△ABC中,BC边的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )