题目内容
1.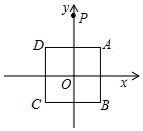 如图,在平面直角坐标系中,正方形ABCD的顶点A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点P(0,2),作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此规律操作下去,则点P2017的坐标为( )
如图,在平面直角坐标系中,正方形ABCD的顶点A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点P(0,2),作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此规律操作下去,则点P2017的坐标为( )| A. | (2,0) | B. | (0,2) | C. | (0,-2) | D. | (-2,0) |
分析 首先求出点P1,P2,P3,P4的坐标,从而发现点的坐标以4为周期,作循环往复的周期变化,即可解决问题.
解答 解:∵点P坐标为(0,2),点A坐标为(1,1),
∴点P关于点A的对称点P1的坐标为(2,0),
点P1关于点B(1,-1)的对称点P2的坐标(0,-2),
点P2关于点C(-1,-1)的对称点P3的坐标为(-2,0),
点P3关于点D(-1,1)的对称点P4的坐标为(0,2),
即点P4与点P重合了;
∵2017=4×504+1,
∴点P2017的坐标与点P1的坐标相同,
∴点P2017的坐标为(2,0),
故选:A.
点评 此题主要考查了点的坐标,解题的关键是首先探索出个别点的坐标的变化规律,然后从特殊到一般去发现一般规律,进而利用规律去解决问题.

练习册系列答案
相关题目
12.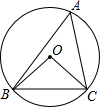 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )| A. | 22.5° | B. | 35° | C. | 45° | D. | 67.5° |
16.在下列命题中:
①同旁内角互补;
②两点确定一条直线;
③两条直线相交,有且只有一个交点;
④若一个角的两边分别与另一个角的两边平行,那么这两个角相等.
其中属于真命题的有( )
①同旁内角互补;
②两点确定一条直线;
③两条直线相交,有且只有一个交点;
④若一个角的两边分别与另一个角的两边平行,那么这两个角相等.
其中属于真命题的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6. 一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
 一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
10.如图1,菱形纸片ABCD的边长为2,∠ABC=60°,将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P(如图2),则六边形AEFCHG面积的最大值是( )
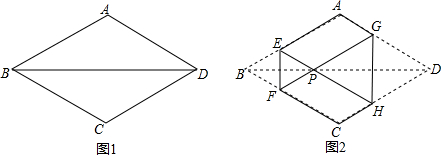

| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | 2-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
11.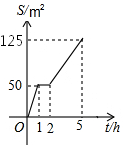 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )| A. | 75m2 | B. | 50m2 | C. | 31.25m2 | D. | 25m2 |
 如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.
如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.