题目内容
2.不等式组$\left\{\begin{array}{l}{-2x-1≤7}\\{-\frac{1}{2}x>1}\end{array}\right.$的最大整数解为-3.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得出其最大整数解.
解答 解:解不等式-2x-1≤7,得:x≥-4,
解不等式-$\frac{1}{2}$x>1,得:x<-2,
∴不等式组的解集为-4≤x<-2,
则不等式组的最大整数解为-3,
故答案为:-3.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
12.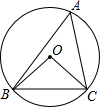 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )| A. | 22.5° | B. | 35° | C. | 45° | D. | 67.5° |
10.如图1,菱形纸片ABCD的边长为2,∠ABC=60°,将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P(如图2),则六边形AEFCHG面积的最大值是( )
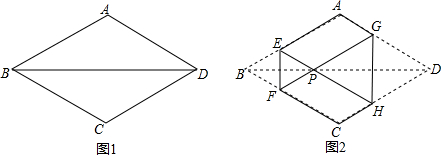

| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | 2-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
14.下列命题中是真命题的是( )
| A. | 如果m是实数,那么m是有理数 | B. | -5没有立方根 | ||
| C. | 互补的角一定的邻补角 | D. | 正数不全是有理数 |
11.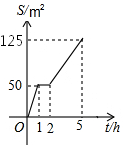 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )| A. | 75m2 | B. | 50m2 | C. | 31.25m2 | D. | 25m2 |
 如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.
如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点. 如图,已知AB⊥BC,BD⊥AC,EC⊥AC,∠1与∠2互补,试说明DF⊥BC的理由.
如图,已知AB⊥BC,BD⊥AC,EC⊥AC,∠1与∠2互补,试说明DF⊥BC的理由. 如图是小强根据全班同学喜爱四类电视节目的人数而绘制的两幅不完整的统计图,则喜爱“体育”节目的人数是10人.
如图是小强根据全班同学喜爱四类电视节目的人数而绘制的两幅不完整的统计图,则喜爱“体育”节目的人数是10人.