题目内容
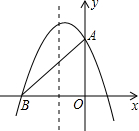 如图,二次函数y=-x2+mx+3的图象与y轴交于点A,与x轴的负半轴交于点B,且△AOB的面积为6.
如图,二次函数y=-x2+mx+3的图象与y轴交于点A,与x轴的负半轴交于点B,且△AOB的面积为6.(1)求该二次函数的表达式;
(2)如果点P在x轴上,且△ABP是等腰三角形,请直接写出点P的坐标.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:
分析:(1)令x=0,即可求得点A的坐标,由△AOB的面积公式可求得OB的长,进而得到点B的坐标;把点B的坐标代入抛物线的解析式,可求得k的值,确定出抛物线解析式;
(2)若△ABP是等腰三角形,且点P在x轴上,故点P的位置有三种情况,由等腰三角形的性质分别求得即可.
(2)若△ABP是等腰三角形,且点P在x轴上,故点P的位置有三种情况,由等腰三角形的性质分别求得即可.
解答:解:(1)由解析式可知,点A的坐标为(0,3).
∵S△OAB=
×BO×3=6,
∴BO=4.
∴B(-4,0),
把点B的坐标(-4,0)代入y=-x2+mx+3,
得-(-4)2+m×(-4)+3=0.
解得m=-
.
∴所求二次函数的解析式为y=-x2-
x+3;
(2)当△ABP是等腰三角形时,需分类讨论:

①如图1,当AB=AP时,点P的坐标为(4,0);
②如图2,当AB=BP时,点P的坐标为(1,0)或(-9,0);
③如图3,当AP=BP时,设点P的坐标为(x,0)根据题意,得
=|x+4|.
解得x=-
.
∴点P的坐标为(-
,0),
综上所述,点P的坐标为(4,0),(1,0),(-9,0),(-
,0).
∵S△OAB=
| 1 |
| 2 |
∴BO=4.
∴B(-4,0),
把点B的坐标(-4,0)代入y=-x2+mx+3,
得-(-4)2+m×(-4)+3=0.
解得m=-
| 13 |
| 4 |
∴所求二次函数的解析式为y=-x2-
| 13 |
| 4 |
(2)当△ABP是等腰三角形时,需分类讨论:

①如图1,当AB=AP时,点P的坐标为(4,0);
②如图2,当AB=BP时,点P的坐标为(1,0)或(-9,0);
③如图3,当AP=BP时,设点P的坐标为(x,0)根据题意,得
| x2+32 |
解得x=-
| 7 |
| 8 |
∴点P的坐标为(-
| 7 |
| 8 |
综上所述,点P的坐标为(4,0),(1,0),(-9,0),(-
| 7 |
| 8 |
点评:本题考查了抛物线与坐标轴的关系,等腰三角形的性质,注意当△ABP是等腰三角形时,点P的位置有三种情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
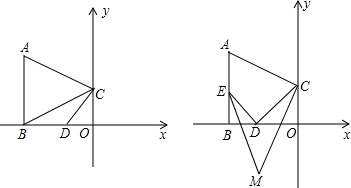
 如图,已知△ADC中,∠A=30°,∠ADC=110°,BE⊥AC,垂足为E,求∠B的度数.
如图,已知△ADC中,∠A=30°,∠ADC=110°,BE⊥AC,垂足为E,求∠B的度数.