题目内容

若
a
x
=
b
y
=
c
z
，求证：
a3
x2
+
b3
y2
+
c3
z2
=
(a+b+c)3
(x+y+z)2
．
考点：分式的混合运算,比例的性质
专题：证明题
分析：设
a
x
=
b
y
=
c
z
=t，则a=xt，y=bt，z=ct，再分别代入式子的左右两边计算后即可得证．
解答：解：设
a
x
=
b
y
=
c
z
=t，则a=xt，y=bt，z=ct，
a3
x2
+
b3
y2
+
c3
z2
=
x3t3
x2
+
y3t3
y2
+
z3t3
z2
=xt3+yt3+zt3=t3（x+y+z），
(a+b+c)3
(x+y+z)2
=
(xt+yt+zt)3
(x+y+z)2
=
t3(x+y+z)3
(x+y+z)2
=t3（x+y+z）．
所以
a3
x2
+
b3
y2
+
c3
z2
=
(a+b+c)3
(x+y+z)2
．
点评：本题考查了分式的混合运算以及比列的性质，关键是设
a
x
=
b
y
=
c
z
=t，则a=xt，y=bt，z=ct．
练习册系列答案
相关题目
计算：
（1）9
1
45
÷
3
2
3
5
×
1
2
2
2
3
；
（2）
8
3
+
1
2
+
0.125
-
6
+
32
；
（3）（
12
6
-
4
18
+
5
3
-
2
）•
6
；
（4）2a
3ab2
-
b
6
27a3
-6ab
a
3
（b≥0）．
试比较（
1
a
）0与（
1
a
）-1（a≠0）大小．
m是绝对值最小的正整数，则m的值是
 
．
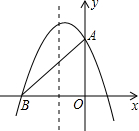如图，二次函数y=-x2+mx+3的图象与y轴交于点A，与x轴的负半轴交于点B，且△AOB的面积为6．
（1）求该二次函数的表达式；
（2）如果点P在x轴上，且△ABP是等腰三角形，请直接写出点P的坐标．
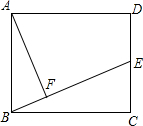在矩形ABCD中，AB=10，BC=12，E为CD的中点，连接B、E，作AF⊥BE，垂足为F，则AF=
 
．
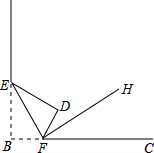如图，将长方形纸片的一角斜折过去，使点B落在点D处，EF为折痕，再把FC折过去与FD重合，FH为折痕，问：
（1）EF与FH有什么样的位置关系？
（2）∠CFH与∠BEF有什么样的数量关系？
数轴上的两点A、B分别表示-7和3，那么A、B两点间的距离是
 
个单位．
如图，已知矩形ABCD的边AB=1，BC=3，现把矩形ABCD绕着它的对称中心旋转，若重叠部分的形状为菱形且面积为S，则S的取值范围为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网