题目内容
已知AB是⊙O的直径，AC是⊙O的切线，A为切点，割线CDF交AB于E，并且满足CD：DE：EF=1：2：1，AC=4，求AB的值．
考点：切割线定理,勾股定理,相交弦定理
专题：
分析：首先利用切割线定理得出CD的长，进而利用勾股定理以及相交线定理得出BE进而得出答案．
解答：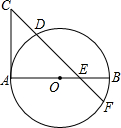
解：如图，∵CD：DE：EF=1：2：1，
设CD=x，DE=2x，EF=x，
则CF=4x，
由切割线定理得：
AC2=CD×CF，
即42=4x2，
解得：x=2，
∴CD=2，DE=4，EF=2，CE=CD+DE=6，
∵AB是⊙O的直径，AC是⊙O的切线，
∴AB⊥AC，
在直角三角形中，AE=
=
=2
，
由相交线定理：AE•EB=DE•EF，
即2
EB=4×2，
解得：BE=
，
故AB=AE+EB=2
+
=
．
解：如图，∵CD：DE：EF=1：2：1，设CD=x，DE=2x，EF=x，
则CF=4x，
由切割线定理得：
AC2=CD×CF，
即42=4x2，
解得：x=2，
∴CD=2，DE=4，EF=2，CE=CD+DE=6，
∵AB是⊙O的直径，AC是⊙O的切线，
∴AB⊥AC，
在直角三角形中，AE=
| CE2-AC2 |
| 62-42 |
| 5 |
由相交线定理：AE•EB=DE•EF，
即2
| 5 |
解得：BE=
4
| ||
| 5 |
故AB=AE+EB=2
| 5 |
4
| ||
| 5 |
14
| ||
| 5 |
点评：此题主要考查了切割线定理、勾股定理以及相交线定理等知识，得出DC的长是解题关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
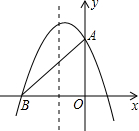如图，二次函数y=-x2+mx+3的图象与y轴交于点A，与x轴的负半轴交于点B，且△AOB的面积为6．
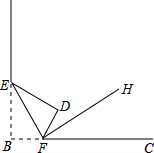如图，将长方形纸片的一角斜折过去，使点B落在点D处，EF为折痕，再把FC折过去与FD重合，FH为折痕，问：
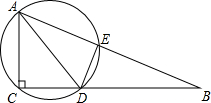如图，在Rt△ABC中，∠ACB=90°，AC=5，CB=12，AD是△ABC的角平分线，过A、C、D三点的圆O与斜边AB交于点E，连接DE．