题目内容
9.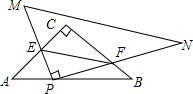 如图,在等腰直角三角形ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,Rt△PMN的直角顶点P在线段AB上,PM、PN分别交于AC、BC于点E、F,PA:PB=1:2,∠BPF=15°,则EF的长为$\frac{2\sqrt{30}}{3}$.
如图,在等腰直角三角形ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,Rt△PMN的直角顶点P在线段AB上,PM、PN分别交于AC、BC于点E、F,PA:PB=1:2,∠BPF=15°,则EF的长为$\frac{2\sqrt{30}}{3}$.
分析 过P作PG⊥BC于G,PD⊥C于D,根据矩形得出CD=PG,CG=PD,求出AP=2,BP=4,解直角三角形求出PE、AD、PG、PF,根据勾股定理求出EF即可.
解答 解:过P作PG⊥BC于G,PD⊥C于D,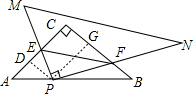
则∠ADP=90°,∠PGF=90°,∠CDP=∠C=∠PGC=90°,
∴四边形CDPG是矩形,
∴CD=PG,CG=PD,
∵在等腰直角三角形ABC中,AC=BC=3$\sqrt{2}$×$\sqrt{2}$=6,
∴AB=$\sqrt{2}$AC=6,∠A=∠B=45°,
∵∠BPF=15°,
∴∠PFG=∠B+∠BPF=60°,
∴∠GPF=30°,
∴PF=2GF,
∵PA:PB=1:2,AB=6,
∴AP=2,BP=4,
∵∠EPF=90°,∠BPF=15°,
∴∠EPA=75°,
∵∠A=45°,∠PDA=90°,
∴∠PDA=45°=∠A,
∴∠EPD=75°-45°=30°,AD=DP,
在Rt△ADP中,AD=PD=AP×sin45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
在Rt△PDE中,DE=PD×tan30°=$\sqrt{2}×\frac{\sqrt{3}}{3}$=$\frac{\sqrt{6}}{3}$,PE=2DE=$\frac{2\sqrt{6}}{3}$,
CD=PG=AC-AD=3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,
在Rt△PGF中,由勾股定理得:GF2+(2$\sqrt{2}$)2=(2GF)2,
解得:GF=$\frac{2\sqrt{6}}{3}$,PF=2GF=$\frac{4\sqrt{6}}{3}$,
在Rt△EPF中,由勾股定理得:EF=$\sqrt{P{E}^{2}+P{F}^{2}}$=$\sqrt{(\frac{2\sqrt{6}}{3})^{2}+(\frac{4\sqrt{6}}{3})^{2}}$=$\frac{2\sqrt{30}}{3}$,
故答案为:$\frac{2\sqrt{30}}{3}$.
点评 本题考查了矩形的性质和判定,勾股定理,解直角三角形的应用,能求出PE和PF的长是解此题的关键.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案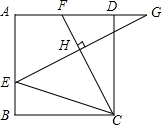 如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )
如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )| A. | 1:1 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1:2 |
| A. |  | B. |  | C. |  | D. |  |
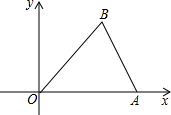 如图,已知A(3,0),B(2,3),将△OAB以点O为位似中心,相似比为2:1,放大得到△OA′B′,则顶点B的对应点B′的坐标为(-4,-6)或(4,6).
如图,已知A(3,0),B(2,3),将△OAB以点O为位似中心,相似比为2:1,放大得到△OA′B′,则顶点B的对应点B′的坐标为(-4,-6)或(4,6).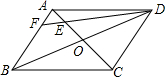 如图,?ABCD的对角线AC,BD相交于点O,点E是AO的中点,连接DE并延长交AB于点F,请探究AF与BF的数量关系,并证明你的结论.
如图,?ABCD的对角线AC,BD相交于点O,点E是AO的中点,连接DE并延长交AB于点F,请探究AF与BF的数量关系,并证明你的结论. 如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,且另外两条边长均为无理数,满足这样的点C共8个.
如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,且另外两条边长均为无理数,满足这样的点C共8个.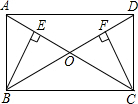 如图,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F.
如图,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F.