题目内容
已知△ABC的面积为S.
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连结DA,试求△ABD的面积(用含S的代数式表示);
(2)如图2,分别延长△ABC的边BC、CA、AB到点D、E、F,使CD=BC、AE=CA、FB=BA,连结DE,EF,FD得到△DEF,试探究△ECD、△FAE和△DBF的面积之间的关系,并对你的结论给予证明;
(3)像(2)中那样,将△ABC各边均顺次延长一倍,连结其端点得到△DEF,叫做将△ABC向外进行了1次倍边扩展,如图3,△MGH是将△ABC向外进行了2次倍边扩展所得到的三角形.问经过多少次倍边扩展后所得三角形的面积会超过2008S?为什么?
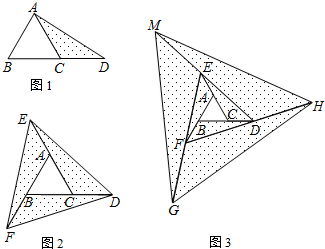
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连结DA,试求△ABD的面积(用含S的代数式表示);
(2)如图2,分别延长△ABC的边BC、CA、AB到点D、E、F,使CD=BC、AE=CA、FB=BA,连结DE,EF,FD得到△DEF,试探究△ECD、△FAE和△DBF的面积之间的关系,并对你的结论给予证明;
(3)像(2)中那样,将△ABC各边均顺次延长一倍,连结其端点得到△DEF,叫做将△ABC向外进行了1次倍边扩展,如图3,△MGH是将△ABC向外进行了2次倍边扩展所得到的三角形.问经过多少次倍边扩展后所得三角形的面积会超过2008S?为什么?

考点:面积及等积变换
专题:
分析:(1)由BC=CD,根据三角形中线的性质,即可得S△ABC=S△ACD=S,则可求得△ABD的面积;
(2)首先连接AD,由CD=BC、AE=CA,易得S△DEA=S△DAC=S△ACD=S△ABC=S,则可求得S△ECD=2S,同理可得S△ECD=S△FAE=S△DBF=2S;
(3)由(2)易得:将△ABC向外进行n次倍边扩展所得到的三角形的面积为:7nS,继而求得答案.
(2)首先连接AD,由CD=BC、AE=CA,易得S△DEA=S△DAC=S△ACD=S△ABC=S,则可求得S△ECD=2S,同理可得S△ECD=S△FAE=S△DBF=2S;
(3)由(2)易得:将△ABC向外进行n次倍边扩展所得到的三角形的面积为:7nS,继而求得答案.
解答: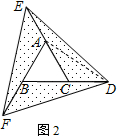 解:(1)∵BC=CD,
解:(1)∵BC=CD,
∴S△ABC=S△ACD=S,
∴S△ABD=2S;
(2)S△ECD=S△FAE=S△DBF.
证明:连接AD,
∵EA=AC,BC=CD,
∴S△DEA=S△DAC=S△ACD=S△ABC=S,
∴S△ECD=2S,
同理:S△FAE=S△FBD=2S,
∴S△ECD=S△FAE=S△DBF.
(3)经过4次倍边扩展后所得三角形的面积会超过2008S.
理由:由(2)可得:S△ECD=S△FAE=S△DBF=2S,
∴S△EFD=S△ECD+S△FAE+S△DBF+S△ABC=2S+2S+2S+S=7S,
∴经过1次倍边扩展后所得面积为原三角形面积的7倍,
即S△EFD=7S,
∵将△ABC向外进行了2次倍边扩展所得到的△MGH可以看成是由△DEF进行了1次倍边扩展所得,
∴S△HMG=7S△EFD=72S,
∴将△ABC向外进行n次倍边扩展所得到的三角形的面积为:7nS,
当n=4时,74S=2401S>2008S,
∴经过4次倍边扩展后所得三角形的面积会超过2008S.
 解:(1)∵BC=CD,
解:(1)∵BC=CD,∴S△ABC=S△ACD=S,
∴S△ABD=2S;
(2)S△ECD=S△FAE=S△DBF.
证明:连接AD,
∵EA=AC,BC=CD,
∴S△DEA=S△DAC=S△ACD=S△ABC=S,
∴S△ECD=2S,
同理:S△FAE=S△FBD=2S,
∴S△ECD=S△FAE=S△DBF.
(3)经过4次倍边扩展后所得三角形的面积会超过2008S.
理由:由(2)可得:S△ECD=S△FAE=S△DBF=2S,
∴S△EFD=S△ECD+S△FAE+S△DBF+S△ABC=2S+2S+2S+S=7S,
∴经过1次倍边扩展后所得面积为原三角形面积的7倍,
即S△EFD=7S,
∵将△ABC向外进行了2次倍边扩展所得到的△MGH可以看成是由△DEF进行了1次倍边扩展所得,
∴S△HMG=7S△EFD=72S,
∴将△ABC向外进行n次倍边扩展所得到的三角形的面积为:7nS,
当n=4时,74S=2401S>2008S,
∴经过4次倍边扩展后所得三角形的面积会超过2008S.
点评:此题考查了三角形中线的性质,属于面积及等积变换问题.此题难度较大,注意得到规律:将△ABC向外进行n次倍边扩展所得到的三角形的面积为:7nS,是解此题的关键.

练习册系列答案
相关题目
 如图,这个图形旋转一周会与原图形重合几次?( )
如图,这个图形旋转一周会与原图形重合几次?( )| A、0 | B、1 | C、2 | D、4 |
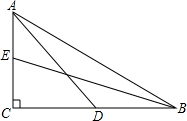 如图,Rt△ABC中,∠C=90°,AD、BE为Rt△ABC的两条中线,AD=6,BE=8,则AB=
如图,Rt△ABC中,∠C=90°,AD、BE为Rt△ABC的两条中线,AD=6,BE=8,则AB=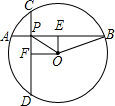 如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为P,OE⊥AB于E,OF⊥CD于F,
如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为P,OE⊥AB于E,OF⊥CD于F, 已知:如图,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F,且BD=CD.
已知:如图,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F,且BD=CD. 如图,三条直线AB,CD,EF相交于一点O,且OF平分∠BOD,那么∠3=∠4吗?为什么?
如图,三条直线AB,CD,EF相交于一点O,且OF平分∠BOD,那么∠3=∠4吗?为什么?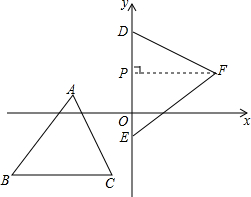 如图,在平面直角坐标系xOy中,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC.若A点的坐标为(-3,1),B、C两点的纵坐标均为-3,D、E两点在y轴上.
如图,在平面直角坐标系xOy中,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC.若A点的坐标为(-3,1),B、C两点的纵坐标均为-3,D、E两点在y轴上. 已知,如图,O是五边形ABCDE内一点,且∠OBC=
已知,如图,O是五边形ABCDE内一点,且∠OBC=