题目内容
已知：如图，AD平分∠BAC，DE⊥AB，DF⊥AC，垂足分别为E，F，且BD=CD．求证：BE=CF．
考点：全等三角形的判定与性质,角平分线的性质
专题：证明题
分析：如图，证明DE=DF，∠E=∠DFC=90°；进而证明Rt△BDE≌Rt△DFC，即可解决问题．
解答：证明：如图，∵AD平分∠BAC，DE⊥AB，DF⊥AC，
∴DE=DF，∠E=∠DFC=90°；
在Rt△BDE和Rt△DFC中，
，
∴Rt△BDE≌Rt△DFC （HL），
∴BE=CF．
证明：如图，∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴DE=DF，∠E=∠DFC=90°；
在Rt△BDE和Rt△DFC中，
|
∴Rt△BDE≌Rt△DFC （HL），
∴BE=CF．
点评：该题主要考查了全等三角形的判定、角平分线的性质及其应用等几何知识点问题；应牢固掌握全等三角形的判定．
练习册系列答案
相关题目
如图，BD⊥AC，CE⊥AB，垂足分别为点D和点E，BD与CE相交于点F，BF=CF．求证：点F在∠BAC的平分线上．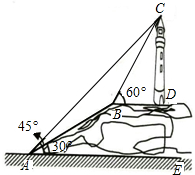
如图，某教学学习小组为了测量山顶上一古灯塔的高度CD，他们在山脚下的点A处测得塔顶C处的仰角为45°，沿着坡角为30°的登山梯AB向上走200米到达山顶B处后，测得塔顶C处的仰角为60°，已知点B与底部D在同一水平线上．
如图，下列结论中，正确的是（ ）| A、∠DAC与∠ACB是一对同位角 |
| B、若∠DAC=∠ACB，则AB∥CD |
| C、∠D与∠DAC是一对同旁内角 |
| D、若∠D=∠B，则AD∥BC |
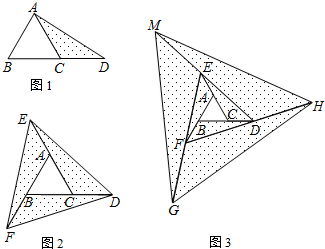
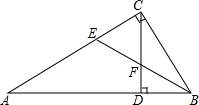如图，已知△ABC中，∠ACB=90°，CD为AB边上的高，∠ABC的平分线BE分别交CD、CA于点F、E，则下列结论正确的