题目内容
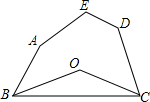 已知,如图,O是五边形ABCDE内一点,且∠OBC=
已知,如图,O是五边形ABCDE内一点,且∠OBC=| 1 |
| 3 |
| 1 |
| 3 |
考点:多边形内角与外角
专题:
分析:首先计算出五边形ABCDE内角和,然后表示出∠ABC+∠DCB=540°-α,再根据角之间的倍分关系可得∠OBC+∠OCB=
(540°-α)=180°-
α,再根据三角形内角和定理可得∠O=180°-(180°-
α)=
α.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:五边形ABCDE内角和为:180°×(5-2)=540°,
∵∠A+∠D+∠E=α,
∴∠ABC+∠DCB=540°-α,
∵∠OBC=
∠ABC,∠OCB=
∠DCB,
∴∠OBC+∠OCB=
(540°-α)=180°-
α,
∵∠O+∠OBC+∠OCB=180°,
∴∠O=180°-(180°-
α)=
α,
故答案为:
α.
∵∠A+∠D+∠E=α,
∴∠ABC+∠DCB=540°-α,
∵∠OBC=
| 1 |
| 3 |
| 1 |
| 3 |
∴∠OBC+∠OCB=
| 1 |
| 3 |
| 1 |
| 3 |
∵∠O+∠OBC+∠OCB=180°,
∴∠O=180°-(180°-
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:此题主要考查了多边形内角和,关键是正确表示出∠OBC+∠OCB=
(540°-α)=180°-
α.
| 1 |
| 3 |
| 1 |
| 3 |

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
下列无理数中,在-4与-3之间的是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
如图是深圳地铁交通图的一部分,小明要坐地铁从世界之窗站到科学馆站,他选择了坐地铁1号线直达,用数学知识解释其选择的原因,可以为( )
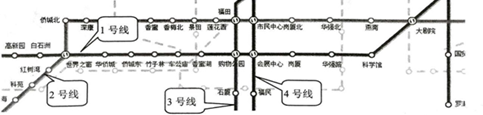

| A、两点之间,线段最短 |
| B、两点确定一条直线 |
| C、两点之间线段的长度,叫做这两点之间的距离 |
| D、过一点有无数条直线 |
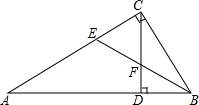
 如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF.求证:点F在∠BAC的平分线上.
如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF.求证:点F在∠BAC的平分线上.
 如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的
如图,已知△ABC中,∠ACB=90°,CD为AB边上的高,∠ABC的平分线BE分别交CD、CA于点F、E,则下列结论正确的 如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点.
如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点.