题目内容
 如图,已知一水坝截面为梯形,坝顶宽为4m.坝高6m,迎水坡的坡度为1:
如图,已知一水坝截面为梯形,坝顶宽为4m.坝高6m,迎水坡的坡度为1:| 3 |
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:过点A、B分别作AE⊥CD,BF⊥CD,可得AE=BF=6m,分别在三角形ACE和三角形BDF中求出CE、DF的长度,继而可求得坝底宽.
解答:
解: 过点A、B分别作AE⊥CD,BF⊥CD,
过点A、B分别作AE⊥CD,BF⊥CD,
则四边形ABFE为矩形,AE=BF=6m,AB=EF=4m,
在Rt△ACE中,
∵i=1:
,
∴CE=6
m,
在Rt△BDF中,
∵∠D=60°,
∴DF=
=2
m,
∴CD=CE+EF+FD=6
+4+2
=8
+4(m).
答:坝底宽为(8
+4)m.
 过点A、B分别作AE⊥CD,BF⊥CD,
过点A、B分别作AE⊥CD,BF⊥CD,则四边形ABFE为矩形,AE=BF=6m,AB=EF=4m,
在Rt△ACE中,
∵i=1:
| 3 |
∴CE=6
| 3 |
在Rt△BDF中,
∵∠D=60°,
∴DF=
| BF |
| tan60° |
| 3 |
∴CD=CE+EF+FD=6
| 3 |
| 3 |
| 3 |
答:坝底宽为(8
| 3 |
点评:本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造直角三角形,利用三角函数求解,难度一般.

练习册系列答案
相关题目
下列命题中的假命题是( )
| A、圆心角的度数与它所对的弧的度数相等 |
| B、等弧所对的弦相等 |
| C、90°的圆周角所对的弦是直径 |
| D、三点确定一个圆 |
 实数a、b在数轴上的位置如图所示,则下列结果正确的是( )
实数a、b在数轴上的位置如图所示,则下列结果正确的是( )| A、a>0 | B、ab>0 |
| C、a-b>0 | D、a+b>0 |
 仔细观察图,认真分析各式,然后解答问题:
仔细观察图,认真分析各式,然后解答问题: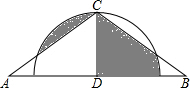 如图,在△ABC中,∠A=30°,AC=BC=12,过点C作CD⊥AB于D,以点D为圆心,CD为半径画半圆,则图中阴影部分的面积为
如图,在△ABC中,∠A=30°,AC=BC=12,过点C作CD⊥AB于D,以点D为圆心,CD为半径画半圆,则图中阴影部分的面积为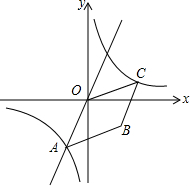 如图,已知正比例函数y=2x与反比例函数的图象交于点A(m,-2)
如图,已知正比例函数y=2x与反比例函数的图象交于点A(m,-2)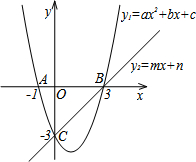 如图,在同一直角坐标系中,抛物线y1=ax2+bx+c与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),直线y2=mx+n与抛物线交于B、C两点.由图象可知:
如图,在同一直角坐标系中,抛物线y1=ax2+bx+c与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),直线y2=mx+n与抛物线交于B、C两点.由图象可知: