题目内容
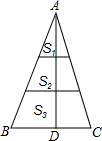如图，将△ABC的高AD三等分，过每个分点作底边的平行线，把△ABC的面积分成三部分S1，S2，S3，则S1：S2：S3=（ ）| A、1：2：3 |
| B、1：4：9 |
| C、1：3：5 |
| D、1：9：25 |
考点：相似三角形的判定与性质
专题：
分析：设AD的三等分点为E、F，由平行可得△AGH∽△APQ∽△ABC，且可得
=
，
=
，可得
=
，
=
，可以得到S1，S2，S3之间的关系，可求出其比例．
| AE |
| AF |
| 1 |
| 2 |
| AE |
| AD |
| 1 |
| 3 |
| S1 |
| S1+S2 |
| 1 |
| 4 |
| S1 |
| S1+S2+S3 |
| 1 |
| 9 |
解答：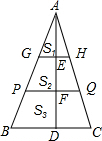
解：
如图，两平行线分别为GH、PQ，与AD交于E、F两点，
∵GH∥PQ∥BC，
∴△AGH∽△APQ∽△ABC，
∵E、F把AD三等分，
∴
=
=
，
=
=
，
∴
=
，
=
，
解得S2=3S1，S3=5S1，
∴S1：S2：S3=1：3：5，
故选C．
解：如图，两平行线分别为GH、PQ，与AD交于E、F两点，
∵GH∥PQ∥BC，
∴△AGH∽△APQ∽△ABC，
∵E、F把AD三等分，
∴
| AG |
| AP |
| AE |
| AF |
| 1 |
| 2 |
| AG |
| AC |
| AE |
| AD |
| 1 |
| 3 |
∴
| S1 |
| S1+S2 |
| 1 |
| 4 |
| S1 |
| S1+S2+S3 |
| 1 |
| 9 |
解得S2=3S1，S3=5S1，
∴S1：S2：S3=1：3：5，
故选C．
点评：本题主要考查相似三角形的判定和性质，利用条件判定出三角形相似，利用相似三角形的面积比等于相似比的平方找到S1，S2，S3之间的关系是解题的关键．
练习册系列答案
相关题目
如图，正十边形A1A2A3A4A5A6A7A8A9A10，连接A7A10，A3A7，则∠A3A7A10的度数为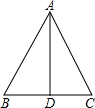
如图，在△ABC中，AB=AC，∠BAD=∠CAD，则下列结论：
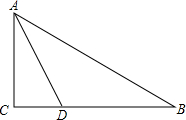已知如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D，
如图，M、N分别为AB、BC的中点，AC=8cm，求MN．
如图，已知线段ab（a＞b）．
如图，在Rt△ABC中，∠C=90°，∠B=30°，c=
如图，∠AOB=30°，OC平分∠AOB，P为OC上的任意一点，PD∥OA，交OB于点D，PE⊥OA于点E，若OD=6cm，则PE的长为