题目内容
 如图,∠AOB=30°,OC平分∠AOB,P为OC上的任意一点,PD∥OA,交OB于点D,PE⊥OA于点E,若OD=6cm,则PE的长为
如图,∠AOB=30°,OC平分∠AOB,P为OC上的任意一点,PD∥OA,交OB于点D,PE⊥OA于点E,若OD=6cm,则PE的长为考点:角平分线的性质,含30度角的直角三角形
专题:
分析:过点P作PF⊥OB于F,根据角平分线上的点到角的两边距离相等可得PF=PE,根据角平分线的定义可得∠AOC=∠BOC,根据两直线平行,内错角相等可得∠AOC=∠OPD,两直线平行,同位角相等可得∠PDF=∠AOB,再求出∠BOC=∠OPD,根据等角对等边可得PD=OD,然后根据直角三角形30°角所对的直角边等于斜边的一半可得PF=
PD.
| 1 |
| 2 |
解答: 解:如图,过点P作PF⊥OB于F,
解:如图,过点P作PF⊥OB于F,
∵OC平分∠AOB,PE⊥OA,
∴PE=PF,
∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵PD∥OA,
∴∠AOC=∠OPD,∠PDF=∠AOB=30°,
∴∠BOC=∠OPD,
∴PD=OD=6cm,
∴PF=
PD=
×6=3cm,
∴PE=PF=3cm.
故答案为:3.
 解:如图,过点P作PF⊥OB于F,
解:如图,过点P作PF⊥OB于F,∵OC平分∠AOB,PE⊥OA,
∴PE=PF,
∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵PD∥OA,
∴∠AOC=∠OPD,∠PDF=∠AOB=30°,
∴∠BOC=∠OPD,
∴PD=OD=6cm,
∴PF=
| 1 |
| 2 |
| 1 |
| 2 |
∴PE=PF=3cm.
故答案为:3.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,平行线的性质,等角对等边的性质,直角三角形30°角所对的直角边等于斜边的一半,熟记各性质并作辅助线是解题的关键.

练习册系列答案
相关题目
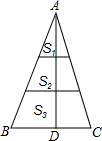 如图,将△ABC的高AD三等分,过每个分点作底边的平行线,把△ABC的面积分成三部分S1,S2,S3,则S1:S2:S3=( )
如图,将△ABC的高AD三等分,过每个分点作底边的平行线,把△ABC的面积分成三部分S1,S2,S3,则S1:S2:S3=( )| A、1:2:3 |
| B、1:4:9 |
| C、1:3:5 |
| D、1:9:25 |
 如图,圆O的直径AB=12,E、F为AB的三等分点,M、N为弧AB上两点,∠MEB=∠NFB=60°,则EM+FN=
如图,圆O的直径AB=12,E、F为AB的三等分点,M、N为弧AB上两点,∠MEB=∠NFB=60°,则EM+FN= 如图,在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上(除点B外)一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,CF交DE于点P.
如图,在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上(除点B外)一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,CF交DE于点P. 如图,点B,E,C,F在同一条直线上,∠B=∠DEF,AB=DE,请补充条件:
如图,点B,E,C,F在同一条直线上,∠B=∠DEF,AB=DE,请补充条件: 作图题(不写作图步骤,保留尺规作图痕迹).
作图题(不写作图步骤,保留尺规作图痕迹). 如图,已知圆内接四边形ABCD中,弧BOD的度数为140°,则∠BAD=
如图,已知圆内接四边形ABCD中,弧BOD的度数为140°,则∠BAD=