题目内容
 如图,在Rt△ABC中,∠C=90°,∠B=30°,c=
如图,在Rt△ABC中,∠C=90°,∠B=30°,c=| 6 |
考点:解直角三角形
专题:
分析:先根据直角三角形的两个锐角互余,求出∠A=90-∠B=60°,再根据30°角所对的直角边等于斜边的一半得出AC=
c=
,然后利用三角函数求出BC.
| 1 |
| 2 |
| ||
| 2 |
解答:解:在Rt△ABC中,∵∠C=90°,∠B=30°,c=
,
∴∠A=90-∠B=60°,AC=
c=
,
∵cosB=
,
∴BC=AB•cos30°=
×
=
.
| 6 |
∴∠A=90-∠B=60°,AC=
| 1 |
| 2 |
| ||
| 2 |
∵cosB=
| BC |
| AB |
∴BC=AB•cos30°=
| 6 |
| ||
| 2 |
3
| ||
| 2 |
点评:本题考查了解直角三角形的定义:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.熟练掌握直角三角形中的边角关系是解题的关键.

练习册系列答案
相关题目
已知圆的内接正六边形的周长为36,那么圆的半径为( )
| A、6 | B、4 | C、3 | D、2 |
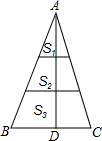 如图,将△ABC的高AD三等分,过每个分点作底边的平行线,把△ABC的面积分成三部分S1,S2,S3,则S1:S2:S3=( )
如图,将△ABC的高AD三等分,过每个分点作底边的平行线,把△ABC的面积分成三部分S1,S2,S3,则S1:S2:S3=( )| A、1:2:3 |
| B、1:4:9 |
| C、1:3:5 |
| D、1:9:25 |
 如图,在矩形ABCD中,AB=3,BC=4.如果BC边上存在点P,使△APD为等腰三角形,那么请求出此时BP的长.
如图,在矩形ABCD中,AB=3,BC=4.如果BC边上存在点P,使△APD为等腰三角形,那么请求出此时BP的长. 如图,圆O的直径AB=12,E、F为AB的三等分点,M、N为弧AB上两点,∠MEB=∠NFB=60°,则EM+FN=
如图,圆O的直径AB=12,E、F为AB的三等分点,M、N为弧AB上两点,∠MEB=∠NFB=60°,则EM+FN= 如图,在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上(除点B外)一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,CF交DE于点P.
如图,在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上(除点B外)一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,CF交DE于点P. 如图,已知圆内接四边形ABCD中,弧BOD的度数为140°,则∠BAD=
如图,已知圆内接四边形ABCD中,弧BOD的度数为140°,则∠BAD=