题目内容
甲、乙、丙三个车队于某日共行驶了21600公里,其中甲车队每辆车平均行驶了325公里,乙车队每辆车平均行驶了250公里,丙车队的每辆车平均行驶了150公里.已知丙车队的车辆数恰好是甲、乙两个车队车辆总数的
,则丙车队最多有多少辆车?
| 1 |
| 3 |
考点:应用类问题
专题:
分析:可设丙车队有y辆车,甲车队有x辆车,则乙车队有3y-x辆车.根据甲、乙、丙三个车队于某日共行驶了21600公里,列出方程325x+250(3y-x)+150y=21600,得到y与x的关系,再根据x,y,3y-x都为正整数,可得y的最大值.
解答:解:设丙车队有y辆车,甲车队有x辆车,则乙车队有3y-x辆车.
甲乙丙三个车队某日分别行驶里程为325x,250(3y-x),150y,由题目已知得:
325x+250(3y-x)+150y=21600,
y=
=24-
,
∵x,y,3y-x都为正整数,
∴可能的取值为:x=12,y=23,3y-x=27;x=24,y=22,3y-x=12;
故y的最大值为23,即丙车队最多有23辆车.
甲乙丙三个车队某日分别行驶里程为325x,250(3y-x),150y,由题目已知得:
325x+250(3y-x)+150y=21600,
y=
| 21600-75x |
| 900 |
| x |
| 12 |
∵x,y,3y-x都为正整数,
∴可能的取值为:x=12,y=23,3y-x=27;x=24,y=22,3y-x=12;
故y的最大值为23,即丙车队最多有23辆车.
点评:考查了应用类问题,解题的关键是根据甲、乙、丙三个车队于某日共行驶了21600公里,列出方程,以及根据整数的性质求解.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
已知圆的内接正六边形的周长为36,那么圆的半径为( )
| A、6 | B、4 | C、3 | D、2 |
在数轴上与原点的距离等于4的点表示的数是( )
| A、4 | B、-4 |
| C、4或-4 | D、无法确定 |
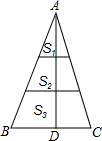 如图,将△ABC的高AD三等分,过每个分点作底边的平行线,把△ABC的面积分成三部分S1,S2,S3,则S1:S2:S3=( )
如图,将△ABC的高AD三等分,过每个分点作底边的平行线,把△ABC的面积分成三部分S1,S2,S3,则S1:S2:S3=( )| A、1:2:3 |
| B、1:4:9 |
| C、1:3:5 |
| D、1:9:25 |
 如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3,那么BC的长为
如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3,那么BC的长为 如图,在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上(除点B外)一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,CF交DE于点P.
如图,在△ABC中,AB=AC,∠BAC=90°,点D为线段BC上(除点B外)一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,CF交DE于点P.