题目内容
 如图,正十边形A1A2A3A4A5A6A7A8A9A10,连接A7A10,A3A7,则∠A3A7A10的度数为
如图,正十边形A1A2A3A4A5A6A7A8A9A10,连接A7A10,A3A7,则∠A3A7A10的度数为考点:正多边形和圆
专题:
分析:如图,作辅助线,首先证明明:
=
⊙O的周长,进而求得∠A3OA10=
×360°=108°,运用圆周角定理问题即可解决.
 |
| A3A1A10 |
| 3 |
| 10 |
| 3 |
| 10 |
解答: 解:如图,设正十边形A1A2A3A4A5A6A7A8A9A10外接圆的圆心为O,
解:如图,设正十边形A1A2A3A4A5A6A7A8A9A10外接圆的圆心为O,
连接OA3、OA10;
由题意知:
=
⊙O的周长,
∴∠A3OA10=
×360°=108°,
∴∠A3A7A10的度数=
×108°=54°,
故答案为54°.
 解:如图,设正十边形A1A2A3A4A5A6A7A8A9A10外接圆的圆心为O,
解:如图,设正十边形A1A2A3A4A5A6A7A8A9A10外接圆的圆心为O,连接OA3、OA10;
由题意知:
 |
| A3A1A10 |
| 3 |
| 10 |
∴∠A3OA10=
| 3 |
| 10 |
∴∠A3A7A10的度数=
| 1 |
| 2 |
故答案为54°.
点评:该题以正多边形和其外接圆为载体,以正多边形及其外接圆的性质为考查的核心构造而成;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
方程x2-x-1=0的两个实根是m、n,则代数式(m2-m+2014)(m+n)的值为( )
| A、2014 | B、0 |
| C、2015 | D、-1 |
 如图,在△ABC中,DE∥BC,
如图,在△ABC中,DE∥BC,| AD |
| BD |
| 1 |
| 2 |
| A、8cm | B、12cm |
| C、11cm | D、10cm |
已知圆的内接正六边形的周长为36,那么圆的半径为( )
| A、6 | B、4 | C、3 | D、2 |
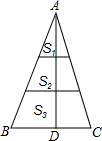 如图,将△ABC的高AD三等分,过每个分点作底边的平行线,把△ABC的面积分成三部分S1,S2,S3,则S1:S2:S3=( )
如图,将△ABC的高AD三等分,过每个分点作底边的平行线,把△ABC的面积分成三部分S1,S2,S3,则S1:S2:S3=( )| A、1:2:3 |
| B、1:4:9 |
| C、1:3:5 |
| D、1:9:25 |
 如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3,那么BC的长为
如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3,那么BC的长为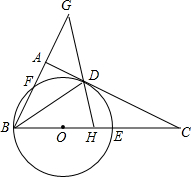 如图,BD为Rt△ABC的角平分线,以BC边上一点O为圆心,过点B、D两点作⊙O,⊙O分别交BC、AB于E、F两点.
如图,BD为Rt△ABC的角平分线,以BC边上一点O为圆心,过点B、D两点作⊙O,⊙O分别交BC、AB于E、F两点.