题目内容
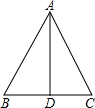 如图,在△ABC中,AB=AC,∠BAD=∠CAD,则下列结论:
如图,在△ABC中,AB=AC,∠BAD=∠CAD,则下列结论:①△ABD≌△ACD;②∠B=∠C;③BD=CD,④AD⊥BC.
其中正确的有
考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:由于AB=AC,∠BAD=∠CAD,利用等边对等角,等腰三角形三线合一定理,可知AD⊥BD,BD=CD,∠B=∠C,从而易证△ABD≌△ACD.
解答:解:∵在△ABC中,AB=AC,∠BAD=∠CAD,
∴AD⊥BD,BD=CD,∠B=∠C,
∴△ABD≌△ACD(SSS).
故答案为①②③④.
∴AD⊥BD,BD=CD,∠B=∠C,
∴△ABD≌△ACD(SSS).
故答案为①②③④.
点评:本题考查了等腰三角形的性质、三角形全等的判定.等腰三角形的角平分线、底边上的中线、底边上的高互相重合.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,DE∥BC,
如图,在△ABC中,DE∥BC,| AD |
| BD |
| 1 |
| 2 |
| A、8cm | B、12cm |
| C、11cm | D、10cm |
已知圆的内接正六边形的周长为36,那么圆的半径为( )
| A、6 | B、4 | C、3 | D、2 |
在数轴上与原点的距离等于4的点表示的数是( )
| A、4 | B、-4 |
| C、4或-4 | D、无法确定 |
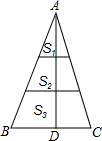 如图,将△ABC的高AD三等分,过每个分点作底边的平行线,把△ABC的面积分成三部分S1,S2,S3,则S1:S2:S3=( )
如图,将△ABC的高AD三等分,过每个分点作底边的平行线,把△ABC的面积分成三部分S1,S2,S3,则S1:S2:S3=( )| A、1:2:3 |
| B、1:4:9 |
| C、1:3:5 |
| D、1:9:25 |
 某校八(4)班每位同学都向汶川地震受灾群众捐款,捐款情况绘制成了扇形统计图,如图所示.求捐款的平均数、众数和中位数.
某校八(4)班每位同学都向汶川地震受灾群众捐款,捐款情况绘制成了扇形统计图,如图所示.求捐款的平均数、众数和中位数. 如图,圆O的直径AB=12,E、F为AB的三等分点,M、N为弧AB上两点,∠MEB=∠NFB=60°,则EM+FN=
如图,圆O的直径AB=12,E、F为AB的三等分点,M、N为弧AB上两点,∠MEB=∠NFB=60°,则EM+FN=