题目内容
18. 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则sin∠BAG=$\frac{\sqrt{10}}{10}$.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则sin∠BAG=$\frac{\sqrt{10}}{10}$.
分析 证明直角△ABG≌直角△AFG,设BG=FG=x,在直角△GCE中利用勾股定理即可列方程求得BG的长,然后在直角△ABG中利用勾股定理求得AG的长,则根据正弦函数的定义求解.
解答 解:∠AFE=∠D=90°,则∠AFG=90°.
在直角△ABG和直角△AFG中,
$\left\{\begin{array}{l}{AB=AF}\\{AG=AG}\end{array}\right.$,
∴直角△ABG≌直角△AFG,
∴BG=FG.
设BG=FG=x,在直角△GCE中,EC=3,GC=6-x,GE=GF+EF=x+3.
则(6-x)2+32=(x+3)2,
解得:x=2.
则在直角△ABG中,AG=$\sqrt{A{B}^{2}+B{G}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$.
则sin∠BGA=$\frac{BG}{AG}$=$\frac{2}{2\sqrt{10}}$=$\frac{\sqrt{10}}{10}$.
故答案是:$\frac{\sqrt{10}}{10}$.
点评 本题考查了图形的折叠、三角函数的定义以及全等三角形的判定与性质,正确证明直角△ABG≌直角△AFG是关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
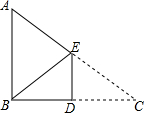 如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为( )
如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为( )