题目内容
4.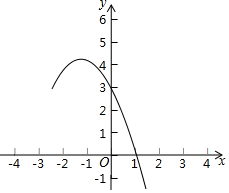 已知抛物线y=-x2+bx+c的部分图象如图所示.
已知抛物线y=-x2+bx+c的部分图象如图所示.(1)求b、c的值.
(2)若抛物线与x轴交于A、B两点(A在B的左侧),顶点为P点,求三角形ABP的面积.
分析 (1)观察函数图象找出点(0,3)、(1,0)在抛物线上,由点的坐标利用待定系数法即可得出结论;
(2)由(1)可得出抛物线解析式,将其变形为顶点式,即可得出点P的坐标,再令y=0即可得出关于x的一元二次方程,解方程即可得出点A、B的坐标,根据三角形的面积公式即可得出结论.
解答 解:(1)观察函数图象可知:点(0,3)、(1,0)在抛物线上,
将点(0,3)、(1,0)代入y=-x2+bx+c中,
得:$\left\{\begin{array}{l}{c=3}\\{-1+b+c=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,
∴b的值为-2,c的值为3.
(2)由(1)可知,抛物线的解析式为y=-x2-2x+3=-(x+1)2+4,
∴抛物线的顶点P的坐标为(-1,4).
令y=0,则有-x2-2x+3=0,
解得:x1=-3,x2=1,
∵A在B的左侧,
∴A(-3,0),B(1,0).
∴S△ABP=$\frac{1}{2}$•(x2-x1)•yp=$\frac{1}{2}$×[1-(-3)]×4=8.
点评 本题考查了抛物线与x轴的交点以及待定系数法求出函数解析式,观察函数图象找出点的坐标再利用待定系数法求出函数解析式是解题的关键.

练习册系列答案
相关题目
19.下列说法正确的是( )
| A. | 完全重合的两个三角形全等 | B. | 面积相等的两个三角形全等 | ||
| C. | 所有的等边三角形全等 | D. | 形状相同的两个三角形全等 |
9.下列结论中正确的是( )
| A. | 数轴上任何一个点都表示唯一的有理数 | |
| B. | 两个无理数的乘积一定是无理数 | |
| C. | 两个无理数之和一定是无理数 | |
| D. | 数轴上的点和实数是一一对应的 |
16.264-1可以被1与10之间的两个整数整除,这两个数是( )
| A. | 3,5 | B. | 5,7 | C. | 7,8 | D. | 7,9 |
 在△ABC中,∠ADB=100°,∠C=80°,∠BAD=∠DAC,BE平分∠ABC,求∠BED的度数.
在△ABC中,∠ADB=100°,∠C=80°,∠BAD=∠DAC,BE平分∠ABC,求∠BED的度数.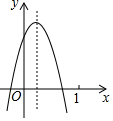 二次函数y=ax2+bx+c(a≠0)的图象如图,结论:①ac<0;②a-b+c<0;③b2-4ac≥0;④y随x的增大而增大,其中正确的个数( )
二次函数y=ax2+bx+c(a≠0)的图象如图,结论:①ac<0;②a-b+c<0;③b2-4ac≥0;④y随x的增大而增大,其中正确的个数( )