题目内容
14. 在△ABC中,∠ADB=100°,∠C=80°,∠BAD=∠DAC,BE平分∠ABC,求∠BED的度数.
在△ABC中,∠ADB=100°,∠C=80°,∠BAD=∠DAC,BE平分∠ABC,求∠BED的度数.
分析 根据三角形外角的性质可得∠DAC=20°,然后再计算出∠EBA=30°,在根据三角形外角的性质可得∠BED的度数.
解答 解:∵∠ADB=100°,∠C=80°,
∴∠DAC=20°,
∵∠BAD=∠DAC,
∴∠BAD=20°,
∴∠DBA=180°-100°-20°=60°,
∵BE平分∠ABC,
∴∠EBA=30°,
∴∠BED=30°+20°=50°.
点评 此题主要考查了三角形内角和,以及外角的性质,关键是掌握三角形的外角等于与它不相邻的两个内角的和,三角形内角和为180°.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
2. 如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
 如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )| A. | 114° | B. | 123° | C. | 132° | D. | 147° |
6.大于-1.8且小于3.1的整数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
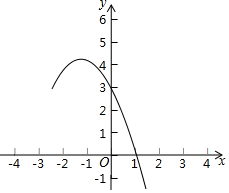 已知抛物线y=-x2+bx+c的部分图象如图所示.
已知抛物线y=-x2+bx+c的部分图象如图所示.