题目内容
13.小明星期天在家里做作业,不小心将方程4-$\frac{x+■}{3}$=x-$\frac{■-1}{2}$中的数字蘸上墨汁,看不清原来的方程,但他知道这两处的数字是相同的,且这个方程的解与方程 $\frac{1-x}{3}$=$\frac{x-1}{2}$也是相同的.你能够知道被墨汁蘸上的数字是多少吗?分析 求出已知方程的解确定出x的值,代入方程计算即可确定出被墨汁蘸上的数字.
解答 解:方程$\frac{1-x}{3}$=$\frac{x-1}{2}$,
去分母得:2(1-x)=3(x-1),
去括号得:2-2x=3x-3,
解得:x=1,
∵方程与方程$\frac{1-x}{3}$=$\frac{x-1}{2}$的解相同,
∴代入x=1到方程4-$\frac{x+■}{3}$=x-$\frac{■-1}{2}$中得到(令 =a),4-$\frac{1+a}{3}$=1-$\frac{a-1}{2}$,
=a),4-$\frac{1+a}{3}$=1-$\frac{a-1}{2}$,
解得:a=-13,
则被墨汁蘸上的数字是-13.
点评 此题考查了同解方程,同解方程即为两个方程的解相同的方程.

练习册系列答案
相关题目
2.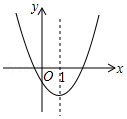 如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a+2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
 如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.①b2>4ac;
②4a+2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ②③④ |
3.下列说法中不正确的是( )
| A. | -a一定是负数 | B. | 0既不是正数,也不是负数 | ||
| C. | 任何正数都大于它们的相反数 | D. | 绝对值小于4的所有整数的和为0 |
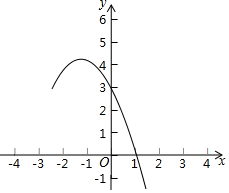 已知抛物线y=-x2+bx+c的部分图象如图所示.
已知抛物线y=-x2+bx+c的部分图象如图所示. 如图,点E是菱形ABCD的边AB上一点,AB=4,∠DAB=60°,过E的直线EF∥AD交 AC、CD于点P、F,过P的直线GH∥AB交AD、BC于点G、H,设AE的长度为x,鱼形(阴影部分)的面积为y,则y关于x的函数解析式是y=$\frac{3\sqrt{3}}{4}$x2-4$\sqrt{3}$x+8$\sqrt{3}$.
如图,点E是菱形ABCD的边AB上一点,AB=4,∠DAB=60°,过E的直线EF∥AD交 AC、CD于点P、F,过P的直线GH∥AB交AD、BC于点G、H,设AE的长度为x,鱼形(阴影部分)的面积为y,则y关于x的函数解析式是y=$\frac{3\sqrt{3}}{4}$x2-4$\sqrt{3}$x+8$\sqrt{3}$.