题目内容
 在平面直角坐标系中,点B的坐标为(2,0),过点B作AB⊥x轴,交y=
在平面直角坐标系中,点B的坐标为(2,0),过点B作AB⊥x轴,交y=| m |
| x |
(1)当
| m |
| 2 |
(2)当n=3时,若点C恰好落在x轴上,求m的值;
(3)当点P运动时,是否存在一个内角为60°的菱形APBC?若存在,求出所有满足条件的m、n的值,并判断点C是否在y=
| m |
| x |
考点:反比例函数综合题
专题:综合题
分析:(1)过点P作PD⊥AB于D,过点C作CE⊥AB于E,易证四边形OPDB是矩形,从而有OP=BD,OB=PD;易证△ADP≌△BEC,则有AD=BE,由xA=xB=2可用m表示出AB,就可用m、n表示出AD即BE的长,问题得以解决.
(2)由条件可得到点A的坐标,代入反比例函数的解析式就可求出m的值.
(3)可分∠APB=60°和∠PAC=60°两种情况讨论,然后运用菱形的性质及勾股定理等知识就可解决问题.
(2)由条件可得到点A的坐标,代入反比例函数的解析式就可求出m的值.
(3)可分∠APB=60°和∠PAC=60°两种情况讨论,然后运用菱形的性质及勾股定理等知识就可解决问题.
解答:解:(1)过点P作PD⊥AB于D,过点C作CE⊥AB于E,如图1.
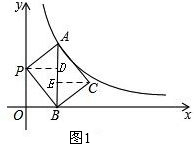
则有∠ADP=∠BEC=90°,∠POB=∠OBD=∠PDB=90°,
∴四边形OPDB是矩形,
∴OP=BD,OB=PD.
∵四边形APBC是平行四边形,
∴AP=BC,AP∥BC,
∴∠PAB=∠CBA.
在△ADP和△BEC中,
,
∴△ADP≌△BEC,
∴AD=BE.
∵点A在函数y=
图象上,xA=xB=2,
∴yA=
即AB=
,
∴BE=AD=AB-BD=AB-OP=
-n,
∴点C的纵坐标为
-n.
(2)当点C恰好落在x轴上时,如图2.
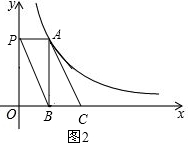
∵四边形APBC是平行四边形,
∴AP∥BC,
∴AB=OP=3,
∴点A的坐标为(2,3).
∵点A在函数y=
图象上,
∴m=2×3=6.
∴m的值为6.
(3)连接PC交AB于点H.
①若∠APB=60°,如图3.
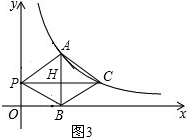
∵四边形APBC是菱形,
∴PH=CH,BH=AH,AB⊥PC,PA=PB,
∴△PAB是等边三角形,
∴PB=AB=2BH,
∴PH=
=
BH.
∵PH=OB=2,
∴
BH=2,
∴BH=
,
∴n=OP=BH=
,点A的坐标为(2,
).
∵点A在函数y=
图象上,
∴m=2×
=
.
此时点C的坐标为(4,
).
∵4×
=
=m,
∴点C在y=
(m>0)的图象上.
②若∠PAC=60°,如图4.
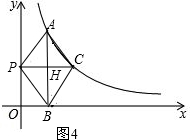
同理可得:m=8
,n=2
,
点C的坐标为(4,2
),在y=
(m>0)的图象上.

则有∠ADP=∠BEC=90°,∠POB=∠OBD=∠PDB=90°,
∴四边形OPDB是矩形,
∴OP=BD,OB=PD.
∵四边形APBC是平行四边形,
∴AP=BC,AP∥BC,
∴∠PAB=∠CBA.
在△ADP和△BEC中,
|
∴△ADP≌△BEC,
∴AD=BE.
∵点A在函数y=
| m |
| x |
∴yA=
| m |
| 2 |
| m |
| 2 |
∴BE=AD=AB-BD=AB-OP=
| m |
| 2 |
∴点C的纵坐标为
| m |
| 2 |
(2)当点C恰好落在x轴上时,如图2.

∵四边形APBC是平行四边形,
∴AP∥BC,
∴AB=OP=3,
∴点A的坐标为(2,3).
∵点A在函数y=
| m |
| x |
∴m=2×3=6.
∴m的值为6.
(3)连接PC交AB于点H.
①若∠APB=60°,如图3.

∵四边形APBC是菱形,
∴PH=CH,BH=AH,AB⊥PC,PA=PB,
∴△PAB是等边三角形,
∴PB=AB=2BH,
∴PH=
| PB2-BH2 |
| 3 |
∵PH=OB=2,
∴
| 3 |
∴BH=
2
| ||
| 3 |
∴n=OP=BH=
2
| ||
| 3 |
4
| ||
| 3 |
∵点A在函数y=
| m |
| x |
∴m=2×
4
| ||
| 3 |
8
| ||
| 3 |
此时点C的坐标为(4,
2
| ||
| 3 |
∵4×
2
| ||
| 3 |
8
| ||
| 3 |
∴点C在y=
| m |
| x |
②若∠PAC=60°,如图4.

同理可得:m=8
| 3 |
| 3 |
点C的坐标为(4,2
| 3 |
| m |
| x |
点评:本题考查了用待定系数法求反比例函数的解析式、矩形的判定与性质、平行四边形的性质、菱形的性质、等边三角形的判定与性质、勾股定理等知识,还考查了分类讨论的数学思想,有一定的综合性.

练习册系列答案
相关题目
方程x2-4x+5=0根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、有一个实数根 |
| D、没有实数根 |
如图,水平地面上有一面积为30cm2的扇形AOB,半径OA=6cm,且OA与地面垂直,在没有滑动的情况下,将扇形向右滚动至OB与地面垂直为止,则点O移动的距离为( )
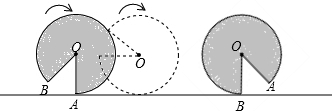

| A、20cm | B、24cm |
| C、10cm | D、30cm |
不等式2x-6>0的解集在数轴上表示正确的是( )
A、 |
B、 |
C、 |
D、 |
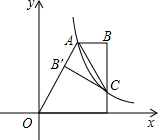 如图,双曲线y=
如图,双曲线y= 如图,四边形ABCD是直角梯形,AD∥BC,∠ABC=90°,过A、B、C三点的⊙O与CD相切于点C,交AD于点G,点E为
如图,四边形ABCD是直角梯形,AD∥BC,∠ABC=90°,过A、B、C三点的⊙O与CD相切于点C,交AD于点G,点E为
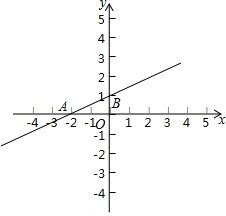 如图,已知直线l:y=kx+b(k≠0)的图象与x轴、y轴交于A、B两点,A(-2,0),B(0,1).
如图,已知直线l:y=kx+b(k≠0)的图象与x轴、y轴交于A、B两点,A(-2,0),B(0,1).