题目内容
如图1,已知O是锐角∠XAY的边AX上的动点,以点O为圆心、R为半径的圆与射线AY相切于点B,交射线OX于点C,过点C作CD⊥BC,CD交AY于点D.
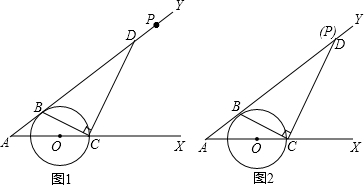
(1)求证:△ABC∽△ACD;
(2)若P是AY上一点,AP=4,且sinA=
.如图2,当点D与点P重合时,求R的值.

(1)求证:△ABC∽△ACD;
(2)若P是AY上一点,AP=4,且sinA=
| 3 |
| 5 |
考点:圆的综合题
专题:
分析:(1)根据切线的性质得到∠ABO=90°,易证∠ABC=∠ACD,从而根据两个角对应相等得到两个三角形相似;
(2)根据(1)中的相似三角形得到对应边的比相等,再结合锐角三角函数的概念,把AD用R表示,根据AD=AP求得R的值.
(2)根据(1)中的相似三角形得到对应边的比相等,再结合锐角三角函数的概念,把AD用R表示,根据AD=AP求得R的值.
解答: (1)证明:如图1,连接OB,
(1)证明:如图1,连接OB,
∵CD⊥BC,
∴∠ADC=90°-∠CBD.
又∵⊙O切AY于点B,
∴OB⊥AB.
∴∠OBC=90°-∠CBD.
∴∠ADC=∠OBC.
又∵在⊙O中,OB=OC=R,
∴∠OBC=∠ACB.
∴∠ACB=∠ADC.
又∵∠A=∠A,
∴△ABC∽△ACD.
(2)解:如图2,连接OB,
∵sinA=
,OB=OC=R,OB⊥AB,
∴在Rt△AOB中,AO=
=
=
R,AB=
=
R.
∴AC=
R+R=
R.
∵△ABC∽△ACD,
∴
=
.
∴
=
.
∴AD=
R.
∵当点D与点P重合时,AD=AP=4,
∴
R=4.
∴R=
.
 (1)证明:如图1,连接OB,
(1)证明:如图1,连接OB,∵CD⊥BC,
∴∠ADC=90°-∠CBD.
又∵⊙O切AY于点B,
∴OB⊥AB.
∴∠OBC=90°-∠CBD.
∴∠ADC=∠OBC.
又∵在⊙O中,OB=OC=R,
∴∠OBC=∠ACB.
∴∠ACB=∠ADC.
又∵∠A=∠A,
∴△ABC∽△ACD.
(2)解:如图2,连接OB,
∵sinA=
| 3 |
| 5 |
∴在Rt△AOB中,AO=
| OB |
| sinA |
| R | ||
|
| 5 |
| 3 |
(
|
| 4 |
| 3 |
∴AC=
| 5 |
| 3 |
| 8 |
| 3 |

∵△ABC∽△ACD,
∴
| AC |
| AB |
| AD |
| AC |
∴
| ||
|
| AD | ||
|
∴AD=
| 16 |
| 3 |
∵当点D与点P重合时,AD=AP=4,
∴
| 16 |
| 3 |
∴R=
| 3 |
| 4 |
点评:此题考查了切线的性质、等腰三角形的性质、勾股定理、相似三角形的判定与性质以及三角函数的性质等知识.此题难度较大,综合性很强,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
要登上12m高的建筑物,为了安全需使梯子底端离建筑物5m,则梯子的长度至少为( )
| A、12m | B、13m |
| C、14m | D、15m |
 正方形ABCD的边AB是⊙O的直径,CF切⊙O于点E,交AD于点F,且切点E在正方形的内部,AE、BE的长是x2-3x+m=0的两实根,令n=AB2.
正方形ABCD的边AB是⊙O的直径,CF切⊙O于点E,交AD于点F,且切点E在正方形的内部,AE、BE的长是x2-3x+m=0的两实根,令n=AB2.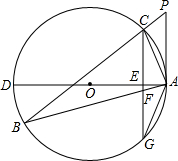 如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.
如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.