题目内容
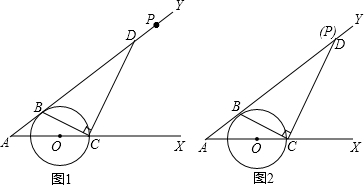
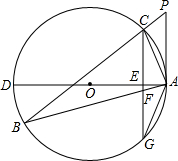 如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.
如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AF•AB;
(3)若⊙O的直径为10,AC=2
| 5 |
| 5 |
考点:圆的综合题
专题:几何综合题
分析:(1)首先连接CD,由AD为⊙O的直径,可得∠ACD=90°,然后由圆周角定理,证得∠B=∠D,由已知∠PAC=∠B,可证得DA⊥PA,继而可证得PA与⊙O相切.
(2)首先连接BG,易证得△AFG∽△AGB,然后由相似三角形的对应边成比例,证得结论;
(3)首先连接BD,由AG2=AF•AB,可求得AF的长,易证得△AEF∽△ABD,即可求得AE的长,继而可求得EF与EG的长,则可求得答案.
(2)首先连接BG,易证得△AFG∽△AGB,然后由相似三角形的对应边成比例,证得结论;
(3)首先连接BD,由AG2=AF•AB,可求得AF的长,易证得△AEF∽△ABD,即可求得AE的长,继而可求得EF与EG的长,则可求得答案.
解答: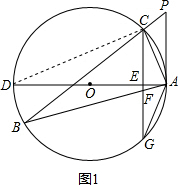 (1)PA与⊙O相切.理由:
(1)PA与⊙O相切.理由:
连接CD,
∵AD为⊙O的直径,
∴∠ACD=90°,
∴∠D+∠CAD=90°,
∵∠B=∠D,∠PAC=∠B,
∴∠PAC=∠D,
∴∠PAC+∠CAD=90°,
即DA⊥PA,
∵点A在圆上,
∴PA与⊙O相切.
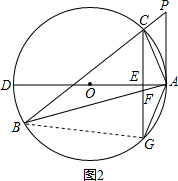 (2)证明:如图2,连接BG,
(2)证明:如图2,连接BG,
∵AD为⊙O的直径,CG⊥AD,
∴
=
,
∴∠AGF=∠ABG,
∵∠GAF=∠BAG,
∴△AGF∽△ABG,
∴AG:AB=AF:AG,
∴AG2=AF•AB;
(3)解:如图3,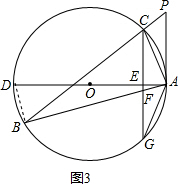 连接BD,
连接BD,
∵AD是直径,
∴∠ABD=90°,
∵AG2=AF•AB,AG=AC=2
,AB=4
,
∴AF=
=
,
∵CG⊥AD,
∴∠AEF=∠ABD=90°,
∵∠EAF=∠BAD,
∴△AEF∽△ABD,
∴
=
,
即
=
,
解得:AE=2,
∴EF=
=1,
∵EG=
=4,
∴FG=EG-EF=4-1=3,
∴S△AFG=
FG•AE=
×3×2=3.
 (1)PA与⊙O相切.理由:
(1)PA与⊙O相切.理由:连接CD,
∵AD为⊙O的直径,
∴∠ACD=90°,
∴∠D+∠CAD=90°,
∵∠B=∠D,∠PAC=∠B,
∴∠PAC=∠D,
∴∠PAC+∠CAD=90°,
即DA⊥PA,
∵点A在圆上,
∴PA与⊙O相切.
 (2)证明:如图2,连接BG,
(2)证明:如图2,连接BG,∵AD为⊙O的直径,CG⊥AD,
∴
 |
| AC |
 |
| AG |
∴∠AGF=∠ABG,
∵∠GAF=∠BAG,
∴△AGF∽△ABG,
∴AG:AB=AF:AG,
∴AG2=AF•AB;
(3)解:如图3,
 连接BD,
连接BD,∵AD是直径,
∴∠ABD=90°,
∵AG2=AF•AB,AG=AC=2
| 5 |
| 5 |
∴AF=
| AG2 |
| AB |
| 5 |
∵CG⊥AD,
∴∠AEF=∠ABD=90°,
∵∠EAF=∠BAD,
∴△AEF∽△ABD,
∴
| AE |
| AB |
| AF |
| AD |
即
| AE | ||
4
|
| ||
| 10 |
解得:AE=2,
∴EF=
| AF2-AE2 |
∵EG=
| AG2-AE2 |
∴FG=EG-EF=4-1=3,
∴S△AFG=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了圆的切线的判定、圆周角定理、垂径定理以及相似三角形的判定与性质.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
下列各式运算正确的是( )
A、
| ||||||
B、3
| ||||||
C、
| ||||||
D、
|
 如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,求证:△ABD为直角三角形.
如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,求证:△ABD为直角三角形. 如图,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE.连接BE,CD.BE与CD有什么数量关系?简单说明理由.
如图,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE.连接BE,CD.BE与CD有什么数量关系?简单说明理由.