Question

20．已知AB为⊙O的直径，点C为$\widehat{AB}$的中点，BD为弦，CE⊥BD于点E，
（1）如图1，求证：CE=DE；
（2）如图2，连接OE，求∠OEB的度数；
（3）如图3，在（2）条件下，延长CE，交直径AB于点F，延长EO，交⊙O于点G，连接BG，CE=2，EF=3，求△EBG的面积．

Answer 1

分析 （1）如图1中，连接CD、OC．只要证明∠CDE=$\frac{1}{2}$∠COB=45°即可．
（2）如图2中，连接OD，OC，只要证明△OED≌△OEC，推出∠OED=∠CEO=135°，即可解决问题．
（3）如图3中，过O作OM⊥BD于M，BN⊥EG于N，则∠EMO=90°，连接OC，设EM=x，则BM=DM=2+x，由EF∥OM，得$\frac{OM}{EF}$=$\frac{BM}{EB}$列出方程即可解决．

解答 （1）证明：如图1中，连接CD、OC．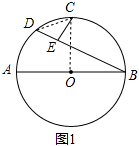

∵点C是$\widehat{AB}$中点，
∴$\widehat{AC}$=$\widehat{BC}$，
∴∠AOC=∠BOC，
∵∠AOC+∠BOC=180°，
∴∠AOC=∠BOC=90°，
∴∠D=45°，
∵CE⊥BD，
∴∠CED=90°，
∴∠D=∠DCE=45°，
∴CE=DE．

（2）证明：如图2中，连接OD，OC

在△OED和△OEC中，
$\left\{\begin{array}{l}{OC=OD}\\{CE=DE}\\{OE=OE}\end{array}\right.$，
∴△OED≌△OEC，
∵∠CED=90°，
∴∠OED=∠CEO=135°，
∴∠OEB=45°．

（3）解：如图3中，过O作OM⊥BD于M，BN⊥EG于N，则∠EMO=90°，连接OC．

∵CE=2，
∴DE=2，
设EM=x，则BM=DM=2+x，
∴BE=2x+2，
∵∠OEB=45°，则BM=DM=2+x，
∴OM=x，
∵∠OEB=45°，
∴∠CEB=∠EMO，
∴EF∥OM．
∴$\frac{OM}{EF}$=$\frac{BM}{EB}$，即$\frac{x}{3}$=$\frac{x+2}{2x+2}$，
解得x=2或（-$\frac{3}{2}$舍弃），
∴OE=2$\sqrt{2}$，BM=4，OM=2，BN=3$\sqrt{2}$，
∴OB=2$\sqrt{5}$
∴EG=OE+OG=2$\sqrt{2}$+2$\sqrt{5}$，
∴S_△EBG=$\frac{1}{2}$•EG•BN=$\frac{1}{2}$（2$\sqrt{2}$+2$\sqrt{5}$）×$3\sqrt{2}$=6+3$\sqrt{10}$．

点评 本题考查圆的综合题、全等三角形的判定和性质、平行线的性质、圆的有关知识，解题的关键是灵活应用这些知识解决问题，学会添加常用辅助线，学会用方程的思想思考问题，属于中考压轴题．