题目内容
13.若$\frac{a}{b}=\frac{c}{d}=\frac{1}{2}(b≠d)$,则下列式子不正确的是( )| A. | $\frac{a+b}{b}=\frac{3}{2}$ | B. | $\frac{a+2c}{b+2d}=2$ | C. | $\frac{a-c}{b-d}=\frac{1}{2}$ | D. | b=2a |
分析 直接利用比例的性质得出a与b,c与d的关系,进而代入各选项求出答案.
解答 解:∵$\frac{a}{b}=\frac{c}{d}=\frac{1}{2}(b≠d)$,
∴b=2a,d=2c,故选项D正确,不合题意;
则$\frac{a+b}{b}$=$\frac{a+2a}{2a}$=$\frac{3}{2}$,故选项A正确,不合题意;
$\frac{a+2c}{b+2d}$=$\frac{a+2c}{2a+4c}$=$\frac{1}{2}$,故选项B错误,符合题意;
$\frac{a-c}{b-d}$=$\frac{a-c}{2a-2d}$=$\frac{1}{2}$,故选项C正确,不合题意;
故选:B.
点评 此题主要考查了比例的性质,正确得出a与b,c与d的关系是解题关键.

练习册系列答案
相关题目
3.下下列各点中,在函数y=2x-3图象上的点是( )
| A. | (0,0) | B. | (1,-1) | C. | (1,1) | D. | (-1,1) |
4.如果单项式-$\frac{1}{2}$xa+2y3与yb-1x是同项式,那么a,b的值分别为( )
| A. | a=-2,b=4 | B. | a=-1,b=2 | C. | a=-1,b=4 | D. | a=-2,b=2 |
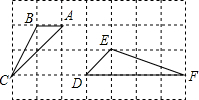 如图,方格纸中每个小正方形的边长都为1,△ABC和△DEF的顶点都在方格纸的格点上.则可判断△ABC和△DEF是否相似:相似(请填“相似”或“不相似”)
如图,方格纸中每个小正方形的边长都为1,△ABC和△DEF的顶点都在方格纸的格点上.则可判断△ABC和△DEF是否相似:相似(请填“相似”或“不相似”)
 如图,矩形纸片ABCD中,AB=3,BC=5,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则FC的长为$\frac{5}{3}$.
如图,矩形纸片ABCD中,AB=3,BC=5,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则FC的长为$\frac{5}{3}$.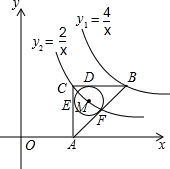 如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=$\frac{4}{x}$的图象经过点B;反比例函数y2=$\frac{2}{x}$的图象经过点C($\sqrt{2}$,m).
如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=$\frac{4}{x}$的图象经过点B;反比例函数y2=$\frac{2}{x}$的图象经过点C($\sqrt{2}$,m).