题目内容
5.为美化小区环境,决定对小区的一块空地实施绿化,现有一长为20m的栅栏,要围成一扇形绿化区域,则该扇形区域的面积的最大值为25m2.分析 首先设扇形区域的半径为xm,则扇形的弧长为(20-2x)m,该扇形区域的面积为ym2,则可得函数:y=$\frac{1}{2}$x(20-2x)=-x2+10x=-(x-5)2+25,继而求得答案.
解答 解:设扇形区域的半径为xm,则扇形的弧长为(20-2x)m,该扇形区域的面积为ym2,
则y=$\frac{1}{2}$x(20-2x)=-x2+10x=-(x-5)2+25,
∴该扇形区域的面积的最大值为25m2.
故答案为:25m2.
点评 此题考查了扇形的面积计算以及二次函数最值问题.注意根据题意得到函数的解析式是关键.

练习册系列答案
相关题目
20. 如图所示,已知AB∥CD,直线EF交AB于点E,交CD于点F,且EG平分∠FEB,∠1=50°,则∠2等于( )
如图所示,已知AB∥CD,直线EF交AB于点E,交CD于点F,且EG平分∠FEB,∠1=50°,则∠2等于( )
 如图所示,已知AB∥CD,直线EF交AB于点E,交CD于点F,且EG平分∠FEB,∠1=50°,则∠2等于( )
如图所示,已知AB∥CD,直线EF交AB于点E,交CD于点F,且EG平分∠FEB,∠1=50°,则∠2等于( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
15.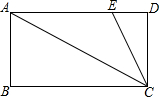 如图,在矩形ABCD中,AB<AD,点E在AD上,且CA平分∠BCE,若△CDE的周长为10,则矩形周长为( )
如图,在矩形ABCD中,AB<AD,点E在AD上,且CA平分∠BCE,若△CDE的周长为10,则矩形周长为( )
 如图,在矩形ABCD中,AB<AD,点E在AD上,且CA平分∠BCE,若△CDE的周长为10,则矩形周长为( )
如图,在矩形ABCD中,AB<AD,点E在AD上,且CA平分∠BCE,若△CDE的周长为10,则矩形周长为( )| A. | 10 | B. | 15 | C. | 20 | D. | 40 |
 一辆汽车和一辆摩托车同时分别从A,B两地去同一城市,它们离A地的路程随时间变化的图象如图所示.当汽车到达目的地时,摩托车距目的地20千米.
一辆汽车和一辆摩托车同时分别从A,B两地去同一城市,它们离A地的路程随时间变化的图象如图所示.当汽车到达目的地时,摩托车距目的地20千米. 如图,直角三角形两直角边的长分别是2、3,阴影部分是一个正方形,设正方形的边长为a,
如图,直角三角形两直角边的长分别是2、3,阴影部分是一个正方形,设正方形的边长为a, 如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.
如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC. A、B两地相距20千米,甲汽车以80千米/小时的速度从A出发,乙汽车以60千米/小时的速度从B出发,两车同时出发且同向而行,问经过几小时,两车相距40千米?
A、B两地相距20千米,甲汽车以80千米/小时的速度从A出发,乙汽车以60千米/小时的速度从B出发,两车同时出发且同向而行,问经过几小时,两车相距40千米?