题目内容
13. 如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.
如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.(1)求证:CF是⊙O的切线.
(2)设⊙O的半径为2,且AC=CE,求AM的长.
分析 (1)连接OC,如图,根据圆周角定理得到∠ACB=90°,则利用∠B=2∠A可计算出∠B=60°,∠A=30°,易得∠E=30°,接着由EF=FC得到∠ECF=∠E=30°,所以∠FCA=60°,加上∠OCA=∠A=30°,所以∠FCO=∠FCA+∠ACO=90°,于是可根据切线的判定得到FC是⊙O的切线;
(2)利用含30度的直角三角形三边的关系.在Rt△ABC中可计算出BC=$\frac{1}{2}$AB=2,AC=$\sqrt{3}$BC=2$\sqrt{3}$,则CE=2$\sqrt{3}$,所以BE=BC+CE=2+2$\sqrt{3}$,然后在Rt△BEM中计算出BM=$\frac{1}{2}$BE=1+$\sqrt{3}$,
再计算AB-BM的值即可.
解答 (1)证明:连接OC,如图,
∵⊙O是△ABC的外接圆,圆心O在AB上,
∴AB是⊙O的直径,
∴∠ACB=90°,
又∵∠B=2∠A,
∴∠B=60°,∠A=30°,
∵EM⊥AB,
∴∠EMB=90°,
在Rt△EMB中,∠B=60°,
∴∠E=30°,
又∵EF=FC,
∴∠ECF=∠E=30°,
又∵∠ECA=90°,
∴∠FCA=60°,
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠FCO=∠FCA+∠ACO=90°,
∴OC⊥CF,
∴FC是⊙O的切线;
(2)解:在Rt△ABC中,∵∠ACB=90°,∠A=30°,AB=4,
∴BC=$\frac{1}{2}$AB=2,AC=$\sqrt{3}$BC=2$\sqrt{3}$,
∵AC=CE,
∴CE=2$\sqrt{3}$,
∴BE=BC+CE=2+2$\sqrt{3}$,
在Rt△BEM中,∠BME=90°,∠E=30°
∴BM=$\frac{1}{2}$BE=1+$\sqrt{3}$,
∴AM=AB-BM=4-1-$\sqrt{3}$=3-$\sqrt{3}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了含30度的直角三角形三边的关系.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{24}{x+2}-\frac{20}{x}$=1 | B. | $\frac{20}{x}-\frac{24}{x+2}$=1 | C. | $\frac{24}{x}-\frac{20}{x+2}$=1 | D. | $\frac{20}{x+2}-\frac{24}{x}$=1 |
| A. | O | B. | L | C. | M | D. | N |
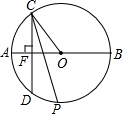 如图,AB为⊙O的直径,从圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,求证:$\widehat{AP}$=$\widehat{BP}$.
如图,AB为⊙O的直径,从圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,求证:$\widehat{AP}$=$\widehat{BP}$. 如图,在△ABC中,AB=AC,AC的垂直平分线交BC于点D,垂足为E,AB=10cm,且△ABD的周长为23cm.求△ABC的周长.
如图,在△ABC中,AB=AC,AC的垂直平分线交BC于点D,垂足为E,AB=10cm,且△ABD的周长为23cm.求△ABC的周长.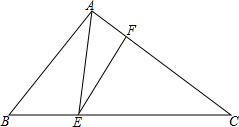 已知:如图,△ABC中,点E、F分别在BC和AC上,BE:BC=1:3,AF:AC=2:5,S△ABC=4,求S△AEF.
已知:如图,△ABC中,点E、F分别在BC和AC上,BE:BC=1:3,AF:AC=2:5,S△ABC=4,求S△AEF.