题目内容
7.求二元一次方程2x+3y=20的非负整数解.分析 要求方程2x+3y=20的非负整数解,就要先将方程做适当变形,根据解为正整数确定其中一个未知数的取值范围,再分析解的情况.
解答 解:由已知得:x=10-$\frac{3}{2}$y
要使x,y都是非负整数,必须满足:10-$\frac{3}{2}$y≥0得0≤y≤$\frac{20}{3}$,
合适的y值只能是0,2,4,6.相应的x值为x=10,7,4,1.
所以有四组解,分别为x=10,y=0;x=7,y=2;x=4,y=4;x=1,y=6.
点评 本题是求不定方程的整数解,先将方程做适当变形,确定其中一个未知数的取值范围,然后列举出适合条件的所有整数值,再求出另一个未知数的值.

练习册系列答案
相关题目
15.一元一次方程a1x2-2x+1=0的两根分别为x1,x2,一元二次方程a2x2-2x+1=0的两根为x3,x4,若0<x1<x3<x4<x2,则a1,a2的大小关系为( )
| A. | a1>a2 | B. | a1=a2 | C. | a1<a2 | D. | 大小无法确定 |
16.若(x+4)(x-5)=x2+mx+n,则m+n=( )
| A. | 21 | B. | -21 | C. | 19 | D. | -19 |
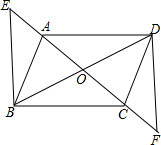 如图,四边形ABCD对角线交于点O,且O为AC中点,AE=CF,DF∥BE,求证:四边形ABCD是平行四边形.
如图,四边形ABCD对角线交于点O,且O为AC中点,AE=CF,DF∥BE,求证:四边形ABCD是平行四边形.