题目内容
12.判断下列几组数据中,可以作为直角三角形的三条边的是( )| A. | 1,2,3 | B. | 2,3,4 | C. | 3,4,5 | D. | 4,5,6 |
分析 要判断三个数是否能是勾股数,只要验证一下,两个较小的数的平方和是否等于最大数的平方,等于就是直角三角形,否则就不是.
解答 解:A、12+22≠32,故不可以作为直角三角形的三条边;
B、22+32≠42,故不可以作为直角三角形的三条边;
C、32+42=52,故可以作为直角三角形的三条边;
D、42+52≠62,故不可以作为直角三角形的三条边.
故选C.
点评 本题主要考查了勾股定理的逆定理的应用.直角三角形的三条边满足勾股定理的逆定理:两条直角边的平方和等于斜边的平方.

练习册系列答案
相关题目
2.2015年12月15日,我国“玉兔号”月球车顺利抵达月球表面,月球离地面平均距离是384400000米,数据38400000用科学记数法表示为( )
| A. | 3.844×106 | B. | 3.844×107 | C. | 3.844×108 | D. | 3.844×109 |
17.已知$\frac{b}{a}$=$\frac{5}{13}$,则$\frac{a-b}{a+b}$的值是( )
| A. | $\frac{8}{13}$ | B. | $\frac{5}{8}$ | C. | $\frac{4}{9}$ | D. | $\frac{9}{4}$ |
4.下列说法中,不正确的是( )
| A. | 棱锥的侧面都是三角形 | B. | 棱柱的上下底面一样大 | ||
| C. | 正方体、长方体都是棱柱 | D. | 四棱锥与四棱柱的棱数一样多 |
1.我国五座名山的海拔高度如下表:
若想根据表中的数据制作成统计图,以便更清楚地对几座名山的高度进行比较,应选用( )
| 山名 | 泰山 | 华山 | 黄山 | 庐山 | 峨眉山 |
| 海拔(m) | 1524 | 1997 | 1873 | 1500 | 3099 |
| A. | 扇形统计图 | B. | 条形统计图 | C. | 折线统计图 | D. | 以上三种都可以 |
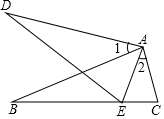 如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.
如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.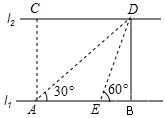 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进60米到达点E(点E在线段AB上),测得∠DEB=60°,求河的宽度.
如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进60米到达点E(点E在线段AB上),测得∠DEB=60°,求河的宽度.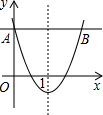 如图,已知二次函数y=x2+bx+c的图象的对称轴是直线x=1,过抛物线上两点的直线AB平行于x轴,若点A的坐标为(0,$\frac{3}{2}$),则点B的坐标为(2,$\frac{3}{2}$).
如图,已知二次函数y=x2+bx+c的图象的对称轴是直线x=1,过抛物线上两点的直线AB平行于x轴,若点A的坐标为(0,$\frac{3}{2}$),则点B的坐标为(2,$\frac{3}{2}$).