题目内容
18.已知三角形3条中位线的比为3:5:6,三角形的周长是112cm,这三条中位线长分别是12cm、20cm、24cm.分析 设三角形3条中位线分别为3x、5x、6x,根据三角形中位线定理求出三角形3条边长,根据周长公式列出方程,解方程即可.
解答 解:设三角形3条中位线分别为3x、5x、6x,
由三角形中位线定理得,三角形3条边分别为6x、10x、12x,
由题意得,6x+10x+12x=112,
解得,x=4,
则3x=12、5x=20、6x=24,
三条中位线长分别是12cm、20cm、24cm,
故答案为:12cm、20cm、24cm.
点评 本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图,在⊙O中,弦AC=2$\sqrt{3}$ cm,C为⊙O上一点,且∠ABC=120°,则⊙O的直径为( )
如图,在⊙O中,弦AC=2$\sqrt{3}$ cm,C为⊙O上一点,且∠ABC=120°,则⊙O的直径为( )
 如图,在⊙O中,弦AC=2$\sqrt{3}$ cm,C为⊙O上一点,且∠ABC=120°,则⊙O的直径为( )
如图,在⊙O中,弦AC=2$\sqrt{3}$ cm,C为⊙O上一点,且∠ABC=120°,则⊙O的直径为( )| A. | 2cm | B. | 4$\sqrt{3}$cm | C. | 4cm | D. | 6cm |
3.下列函数中自变量取值范围选取错误的是( )
| A. | y=$\frac{1}{x-1}$中x≠0 | B. | y=x2中x取全体实数 | ||
| C. | y=$\frac{1}{x+1}$中x≠-1 | D. | y=$\sqrt{x-1}$中x≥1 |
8.有8筐白菜,现进行检测,结果称重如下(单位:千克):27,24,23,28,21,26,22,27,为了求得8筐样品的总质量,我们可以选取的一个恰当的基准数进行简化运算.
(1)你认为选取的一个恰当的基准数为26;
(2)根据你选取的基准数,用正、负数填写如表;
(3)这8筐水果的总质量是多少?
| 原质量 | 27 | 24 | 23 | 28 | 21 | 26 | 22 | 27 |
| 与基准数的差距 | 1 | -2 | -3 | 2 | -5 | 0 | -4 | 1 |
(2)根据你选取的基准数,用正、负数填写如表;
(3)这8筐水果的总质量是多少?
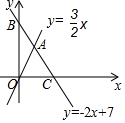 如图,直线y=-2x+7与x轴、y轴分别相交于点C、B,与直线y=$\frac{3}{2}$x相交于点A.
如图,直线y=-2x+7与x轴、y轴分别相交于点C、B,与直线y=$\frac{3}{2}$x相交于点A. 如图,直线:y=$\frac{4}{3}$x与直线y=-x+7相交于点A.
如图,直线:y=$\frac{4}{3}$x与直线y=-x+7相交于点A.