题目内容
7.在△ABC中,AB=9,AC=12,BC=18,D是AC边上一点,DC=$\frac{2}{3}$AC,在AB边上取一点E,连接DE,若两个三角形相似,则DE的长为6或8.分析 分AD与AC是对应边和AD与AB是对应边,根据相似三角形对应边成比例列式求解即可.
解答 解:∵DC=$\frac{2}{3}$AC,
∴$\frac{AD}{AC}$=$\frac{1}{3}$,又AC=12,
∴AD=4,
当△ADE∽△ABC时,$\frac{DE}{BC}$=$\frac{AD}{AB}$,即$\frac{DE}{18}$=$\frac{4}{9}$,
解得,DE=8,
当△AED∽△ABC时,$\frac{DE}{BC}$=$\frac{AD}{AC}$,即$\frac{DE}{18}$=$\frac{1}{3}$,
解得,DE=6,
故答案为:6或8.
点评 本题考查了相似三角形的性质,掌握相似三角形对应边成比例的性质,根据对应边不明确,注意分情况讨论求解.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
15. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )| A. | 20° | B. | 40° | C. | 80° | D. | 70° |
19.为了求1+3+32+33+…+32011的值,可令S=1+3+32+33+…+32011,则3S=3+32+33+…+32012,因此3S-S=32012-1,所以S=$\frac{{3}^{2012}-1}{2}$,仿照以上推理计算出1+7+72+73+…+72015的值是( )
| A. | $\frac{{7}^{2015}-1}{2}$ | B. | $\frac{{7}^{2016}-1}{2}$ | C. | $\frac{{7}^{2015}-1}{6}$ | D. | $\frac{{7}^{2016}-1}{6}$ |
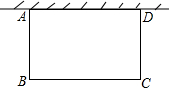 如图,一边靠学校院墙,其他三边用12m长的篱笆围成一个矩形花圃,设矩形ABCD的边AB=xm,面积为S m2.
如图,一边靠学校院墙,其他三边用12m长的篱笆围成一个矩形花圃,设矩形ABCD的边AB=xm,面积为S m2.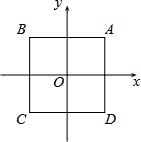 如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.
如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.