题目内容
8.有8筐白菜,现进行检测,结果称重如下(单位:千克):27,24,23,28,21,26,22,27,为了求得8筐样品的总质量,我们可以选取的一个恰当的基准数进行简化运算.| 原质量 | 27 | 24 | 23 | 28 | 21 | 26 | 22 | 27 |
| 与基准数的差距 | 1 | -2 | -3 | 2 | -5 | 0 | -4 | 1 |
(2)根据你选取的基准数,用正、负数填写如表;
(3)这8筐水果的总质量是多少?
分析 (1)我选取的一个恰当的基准数为26;
(2)根据选取的基准数,分别用每次的称重结果减去26,用正、负数填写如表即可;
(3)把这8筐水果的质量与基准数的差距相加,再用它加上26×8,求出这8筐水果的总质量是多少即可.
解答 解:(1)我选取的一个恰当的基准数为26;
(2)27-26=1,24-26=-2,23-26=-3,28-26=2,21-26=-5,26-26=0,22-26=-4,27-26=1,
| 原质量 | 27 | 24 | 23 | 28 | 21 | 26 | 22 | 27 |
| 与基准数的差距 | 1 | -2 | -3 | 2 | -5 | 0 | -4 | 1 |
=-10+208
=198(千克)
答:这8筐水果的总质量是198千克.
故答案为:26.
点评 此题主要考查了负数的意义和应用,以及正、负数的运算,要熟练掌握运算方法.

练习册系列答案
相关题目
19.为了求1+3+32+33+…+32011的值,可令S=1+3+32+33+…+32011,则3S=3+32+33+…+32012,因此3S-S=32012-1,所以S=$\frac{{3}^{2012}-1}{2}$,仿照以上推理计算出1+7+72+73+…+72015的值是( )
| A. | $\frac{{7}^{2015}-1}{2}$ | B. | $\frac{{7}^{2016}-1}{2}$ | C. | $\frac{{7}^{2015}-1}{6}$ | D. | $\frac{{7}^{2016}-1}{6}$ |
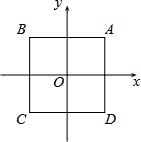 如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.
如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.