题目内容
8. 如图,在⊙O中,弦AC=2$\sqrt{3}$ cm,C为⊙O上一点,且∠ABC=120°,则⊙O的直径为( )
如图,在⊙O中,弦AC=2$\sqrt{3}$ cm,C为⊙O上一点,且∠ABC=120°,则⊙O的直径为( )| A. | 2cm | B. | 4$\sqrt{3}$cm | C. | 4cm | D. | 6cm |
分析 作直径AD,根据直径所对的圆周角是直角,构建直角三角形,由圆内接四边形对角互补得:∠ADC=180°-120°=60°,利用60°的三角函数值求直径的长.
解答  解:作直径AD,交⊙O于D,连接CD,
解:作直径AD,交⊙O于D,连接CD,
∴∠ACD=90°,
∵∠ABC=120°,
∴∠ADC=180°-120°=60°,
在Rt△ACD中,sin∠ADC=sin60°=$\frac{AC}{AD}$,
∴$\frac{2\sqrt{3}}{AD}$=$\frac{\sqrt{3}}{2}$,
∴AD=4,
则⊙O的直径为4cm;
故选C.
点评 本题考查了圆内接四边形的性质、圆周角定理和特殊的三角函数值,根据圆周角定理:直径所对的圆周角是直角构建直角三角形是关键,熟练掌握圆内接四边形对角互补,因此本题的突破口在∠ABC=120°上,方法有很多,不同的辅助线作法,解题思路也不同,可以作AC的弦心距,根据垂径定理来求.

练习册系列答案
相关题目
3.某市某公交车从起点到终点共有六个站,一辆公交车由起点开往终点,在起点站始发时上了部分乘客,从第二站开始下车、上车的乘客数如表:
(1)求本趟公交车在起点站上车的人数;
(2)若公交车的收费标准是上车每人2元,计算此趟公交车从起点到终点的总收入?
| 站次 人数 | 二 | 三 | 四 | 五 | 六 |
| 下车(人) | 3 | 6 | 10 | 7 | 19 |
| 上车(人) | 12 | 10 | 9 | 4 | 0 |
(2)若公交车的收费标准是上车每人2元,计算此趟公交车从起点到终点的总收入?
20.某股民在上周星期五买进某种股票,每股80元.如表是本周每日该股票的涨跌情况(单位:元):
星期五收盘时每股64元.
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +6 | -4.5 | +5 | -3.5 | -7 |
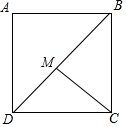 如图,在正方形ABCD中,M是对角线BD上一点,若AB=$\sqrt{2}$,则MD+2MC的最小值是$\sqrt{3}$+1,此时∠BMC=60度.
如图,在正方形ABCD中,M是对角线BD上一点,若AB=$\sqrt{2}$,则MD+2MC的最小值是$\sqrt{3}$+1,此时∠BMC=60度.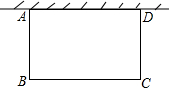 如图,一边靠学校院墙,其他三边用12m长的篱笆围成一个矩形花圃,设矩形ABCD的边AB=xm,面积为S m2.
如图,一边靠学校院墙,其他三边用12m长的篱笆围成一个矩形花圃,设矩形ABCD的边AB=xm,面积为S m2.