题目内容
12.二次函数y=ax2+2x+3与x轴有2个交点,则a的取值范围是( )| A. | $a≤\frac{1}{3}$ | B. | $a≥\frac{1}{3}$ | C. | $a>\frac{1}{3}$ | D. | $a<\frac{1}{3}$且a≠0 |
分析 根据二次函数的定义和抛物线与x轴的交点问题得到a≠0且△=22-4a×3>0,然后求出两不等式的公共部分即可.
解答 解:根据题意得a≠0且△=22-4a×3>0,
解得a<$\frac{1}{3}$且a≠0.
故选D.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.解题时不要忘了a≠0.

练习册系列答案
相关题目
4.国家统计局初步测算,2011年中国国内生产总值(GDP)471564亿元,比上年增长9.2%.其中471564亿用科学记数法表示记为(保留3个有效数字)( )
| A. | 4.71×1013 | B. | 4.72×1013 | C. | 4.71×1012 | D. | 0.472×1014 |
2.直线y=kx+3过点(-2,0),则k的值是( )
| A. | -2 | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -3 |
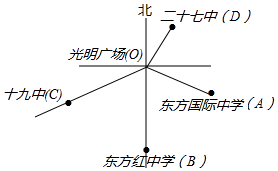 小明在光明广场(点O)绘制了市内几座学校相对广场的位置简图,(图中1cm表示5km),东方红中学在广场正南方向,测得OA=1.7cm,OB=2cm,OC=2cm,OD=1.4cm,∠AOC=123°18′,∠BOA=68°24′,∠AOD=88°28′,如何确定每个学校的具体位置?
小明在光明广场(点O)绘制了市内几座学校相对广场的位置简图,(图中1cm表示5km),东方红中学在广场正南方向,测得OA=1.7cm,OB=2cm,OC=2cm,OD=1.4cm,∠AOC=123°18′,∠BOA=68°24′,∠AOD=88°28′,如何确定每个学校的具体位置?
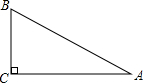 如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.
如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.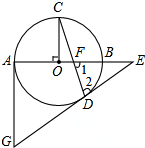 如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上找点E,连接ED,使得∠1=∠2,过点A作⊙O的切线与ED的延长线相交于点G
如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上找点E,连接ED,使得∠1=∠2,过点A作⊙O的切线与ED的延长线相交于点G