题目内容
某校在校内为见义勇为基金会开展了一次捐款活动,学生会随机调查了部分学生的捐款金额,绘制了如下统计图1和统计图2,请根据相关信息,解答下列问题:
(1)直接写出样本中学生捐款金额的众数和中位数,及统计图1中“15元”部分扇形圆心角的度数;
(2)求本次被调查学生的人均捐款金额;
(3)若随机调查该校一名学生,估计该生捐款金额不低于20元的概率.

(1)直接写出样本中学生捐款金额的众数和中位数,及统计图1中“15元”部分扇形圆心角的度数;
(2)求本次被调查学生的人均捐款金额;
(3)若随机调查该校一名学生,估计该生捐款金额不低于20元的概率.
考点:条形统计图,扇形统计图,加权平均数,概率公式
专题:
分析:(1)根据众数、中位数的定义即可求得众数和中位数,利用360°乘以对应的百分比即可求得圆心角的度数;
(2)利用加权平均数公式即可求解;
(3)利用概率公式即可求解.
(2)利用加权平均数公式即可求解;
(3)利用概率公式即可求解.
解答:解:(1)众数10元,中位数 15元,“15元”部分扇形圆心角的度数是:360°×(1-32%-8%-16%-24%)=72°.
(2)解法一:5×8%+10×32%+15×20%+20×24%+30×16%
=16.2(元).
答:人均捐款金额为16.2元.
解法二:
=16.2(元).
答:人均捐款金额为16.2元.
(3)P(不低于20元)=
=
.
答:在该校随机调查一个学生捐款金额不低于20元的概率为
.
(2)解法一:5×8%+10×32%+15×20%+20×24%+30×16%
=16.2(元).
答:人均捐款金额为16.2元.
解法二:
| 4×5+10×16+15×10+20×12+30×8 |
| 4+16+10+12+8 |
答:人均捐款金额为16.2元.
(3)P(不低于20元)=
| 12+8 |
| 50 |
| 2 |
| 5 |
答:在该校随机调查一个学生捐款金额不低于20元的概率为
| 2 |
| 5 |
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
 如图,数轴上有a,b两个数,则下列各式中,不正确的是( )
如图,数轴上有a,b两个数,则下列各式中,不正确的是( )| A、a<0 | B、b>0 |
| C、a>b | D、a<b |
下列计算正确的是( )
A、5
| ||||||
B、2
| ||||||
C、
| ||||||
D、
|

 已知:如图,在△ABC中,∠C=90°,点D、E分别AB、CB延长线上的点,CE=9,AD=15,连接DE.若BC=6,AC=8,求证:△ABC∽△DBE.
已知:如图,在△ABC中,∠C=90°,点D、E分别AB、CB延长线上的点,CE=9,AD=15,连接DE.若BC=6,AC=8,求证:△ABC∽△DBE. 如图,已知∠A=∠C,∠E=∠F,那么AB∥CD吗?为什么?
如图,已知∠A=∠C,∠E=∠F,那么AB∥CD吗?为什么?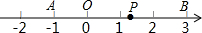 如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x.
如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x.