��Ŀ����
2����֪������L1��y=-$\frac{1}{2}$x2�Ƶ㣨0��-0.5����ת180��õ�������L2��y=ax2+c����1����������L2�Ľ���ʽ��
��2����ͼ����������L2����ƽ�Ƶõ�������L3��y=ax2-$\frac{3}{2}$x-2��������L3 ��x�ύ�ڵ�A��B����y�ύ�ڵ�C����������L3���Ƿ����һ��P��x�����Ƿ����һ��Q��ʹ���Ե�A��C��P��QΪ������ı���Ϊƽ���ı��Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ������1���е������߾����ϡ���ƽ�Ƶõ�������L4��y=ax2+k��һ����OMN�Ķ���O������ԭ��O������N��x���������ϣ���M�ڵ�һ���ޣ��ҡ�MON=45�㣬��N������Ϊ��2��0������������L4������OMN�ı߽��������������㣬��ʵ��k��ȡֵ��Χ��
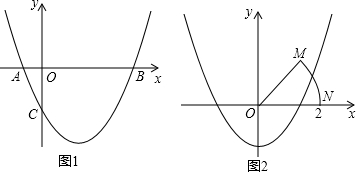
���� ��1�����ݶԳ����ҳ�ԭ�㣨0��0�����ڣ�0��-0.5���ĶԳƵ㣬�ɴ˿ɵó�������L2��y=ax2+c�Ķ���Ϊ��0��-1�����ٽ����ת�����ʼ��ɵó�a��ֵ�����붥�����꼴�ɵó�������L2�Ľ���ʽ��
��2��������ڣ���ϣ�1���ҳ�������L3�Ľ���ʽ���ֱ����x=0��y=0�ҳ���A��C�����꣬�ٷ����߶�ACΪ�Խ��ߺ����߶�ACΪ������������ǣ�����ƽ���ı��ε������ҳ���P��Q�����꣬��ϵ�P��������L3�ϣ����ɵó���Q�����ꣻ
��3���ҳ�����N��������L4��ʱk��ֵ���ٸ�����������ֱ��OM�������ø����б�ʽ�ҳ���ʱ��kֵ���ҳ��е�ĺ����꣬��ϵ�M������ɵó���ʱ�е����߶�OM�ϣ��ۺ�����kֵ���ɵó����ۣ�
��� �⣺��1��ԭ�㣨0��0�����ڵ㣨0��-0.5���ĶԳƵ�Ϊ��0��-1����
��������L2��y=ax2+c�Ķ���Ϊ��0��-1����
������ת�����ʿ�֪��a=-��-$\frac{1}{2}$��=$\frac{1}{2}$��
���㣨0��-1������y=$\frac{1}{2}$x2+c�У��ã�c=-1��
��������L2�Ľ���ʽΪy=$\frac{1}{2}$x2-1��
��2��������ڣ����Q������Ϊ��m��0����
�ɣ�1����֪��������L3��y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2��
��y=0ʱ����$\frac{1}{2}$x2-$\frac{3}{2}$x-2=0��
��ã�x1=-1��x2=4��
��A��-1��0����B��4��0����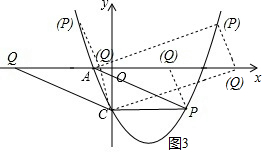
��x=0ʱ��y=-2��
��C��0��-2����
�Ե�A��C��P��QΪ������ı���Ϊƽ���ı��η������������ͼ3��ʾ����
�ٵ��߶�ACΪ�Խ���ʱ����AQ��x���ϣ�
��CP��AQ��x�ᣮ
��y=-2ʱ����$\frac{1}{2}$x2-$\frac{3}{2}$x-2=-2��
��ã�x=3��x=0����ȥ����
��P��3��-2����
��A��-1��0����C��0��-2����
���ʱ��Q������Ϊ��-1+0-3��0-2-��-2����������-4��0����
�ڵ��߶�ACΪ��ʱ����A��-1��0����C��0��-2����Q��m��0����
���P��������m+1��-2����m-1��2����
��y=-2ʱ����$\frac{1}{2}$x2-$\frac{3}{2}$x-2=-2��
��ã�x=3��x=0����ȥ����
��m+1=3����ã�m=2��
��y=2ʱ����$\frac{1}{2}$x2-$\frac{3}{2}$x-2=2��
��ã�x=$\frac{3��\sqrt{41}}{2}$��
��m-1=$\frac{3��\sqrt{41}}{2}$����ã�m=$\frac{5��\sqrt{41}}{2}$��
���Ͽ�֪��������L3�ϴ���һ��P��x���ϴ���һ��Q��ʹ���Ե�A��C��P��QΪ������ı���Ϊƽ���ı��Σ���ʱ��Q������Ϊ��2��0����-4��0����$\frac{5+\sqrt{41}}{2}$��0����$\frac{5-\sqrt{41}}{2}$��0����
��3���ɣ�1����֪��������L4��y=$\frac{1}{2}$x2+k��
����M��ME��x���ڵ�E����ͼ4��ʾ��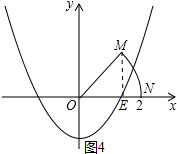
��OM=2����MOE=45�㣬
���MOEΪ����ֱ�������Σ�
��OE=ME=$\frac{\sqrt{2}}{2}$OM=$\sqrt{2}$��
���M��������$\sqrt{2}$��$\sqrt{2}$����
��ֱ��OM�Ľ���ʽΪy=x��
����N��2��0����������L4��y=$\frac{1}{2}$x2+k��ʱ����0=$\frac{1}{2}$��22+k��
��ã�k=-2��
��������L4��y=$\frac{1}{2}$x2+k��ֱ��OM����ʱ����y=x����y=$\frac{1}{2}$x2+k�ã�x2-2x+2k=0��
��=��-2��2-4��2k=0����ã�k=$\frac{1}{2}$��
��k=$\frac{1}{2}$����x2-2x+2k=0�ã�x2-2x+1=��x-1��2=0��
��ã�x=1��
��0��1��$\sqrt{2}$��
�൱����ʱ���е����߶�OM�ϣ�
����������L4������OMN�ı߽��������������㣬��ʵ��k��ȡֵ��ΧΪ-2��k��$\frac{1}{2}$��
���� ���⿼������ת�����ʡ�ƽ���ı��ε����ʡ����κ���ͼ���ϵ�����������Լ������б�ʽ������Ĺؼ��ǣ���1���ҳ�������L2�Ķ��������Լ�������ϵ������2�������߶�ACΪ�Խ��ߺ����߶�ACΪ������������ǣ���3���ҳ�������L4����N����ֱ��OM����ʱ��kֵ�����������е��⣬�ѶȲ������������Ŀʱ������ƽ���ߵ����ʽ����������������ʾ�����ĸ�����������ǹؼ���

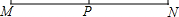 ��ͼ����֪�߶�MN�T6cm����P��MN���е㣮�ֱ���M��NΪԲ�ģ�r1cm��r2cmΪ�뾶��Բ������P�ڡ�M�ڣ����ڡ�N�⣮��r1�ķ�Χ��r1��3��r2�ķ�Χ��0��r2��3��
��ͼ����֪�߶�MN�T6cm����P��MN���е㣮�ֱ���M��NΪԲ�ģ�r1cm��r2cmΪ�뾶��Բ������P�ڡ�M�ڣ����ڡ�N�⣮��r1�ķ�Χ��r1��3��r2�ķ�Χ��0��r2��3��