题目内容
北京两会期间,记者随机抽取参会的部分代表,对他们某天发表提议的次数进行统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发表提议的人数的比为5:2,请结合图中相关数据回答下列问题: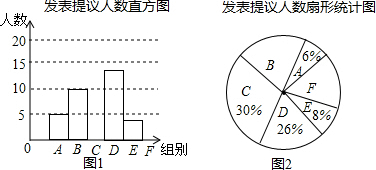
(1)求出样本容量,并补全直方图;
(2)会议期间组织1700名代表调研,请估计在这一天里发表提议次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好是一男一女的概率.

| 发表提议次数“n” | |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
(2)会议期间组织1700名代表调研,请估计在这一天里发表提议次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好是一男一女的概率.
考点:频数(率)分布直方图,频数(率)分布表,扇形统计图,列表法与树状图法
专题:
分析:(1)根据知B、E两组发表提议的人数的比为5:2,即可求得B组的百分比,然后根据B组有10人,据此即可求得总人数,即样本容量,然后根据百分比的意义求得F组的人数,从而补全直方图;
(2)利用总人数乘以对应的百分比即可求解;
(3)利用列举法即可求得总的可能结果,然后利用概率公式求解.
(2)利用总人数乘以对应的百分比即可求解;
(3)利用列举法即可求得总的可能结果,然后利用概率公式求解.
解答:解:(1)B组所占的百分比是x,则x:8%=5:2,解得:x=20%,
则样本容量是:10÷20%=50,则C组的人数是:50×30%=15(人),
F组的人数是:50(1-6%-20%-30%-26%-8%)=5(人).
 ;
;
(2)发表提议次数不少于12次的人数是:1700×(8%+10%)=306(人);
(3)E组的人数是:50×8%=4(人),
A组的人数是:50×6%=3(人),
 ,
,
共有12种情况,所抽的两位代表恰好是一男一女的有6种情况,则概率是:
=
.
则样本容量是:10÷20%=50,则C组的人数是:50×30%=15(人),
F组的人数是:50(1-6%-20%-30%-26%-8%)=5(人).
 ;
;(2)发表提议次数不少于12次的人数是:1700×(8%+10%)=306(人);
(3)E组的人数是:50×8%=4(人),
A组的人数是:50×6%=3(人),
 ,
,共有12种情况,所抽的两位代表恰好是一男一女的有6种情况,则概率是:
| 6 |
| 12 |
| 1 |
| 2 |
点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若⊙O的面积为25π,在同一平面内有一个点P,且点P到圆心O的距离为4.9,则点P与⊙O的位置关系为( )
| A、点P在⊙O外 |
| B、点P在⊙O上 |
| C、点P在⊙O内 |
| D、无法确定 |
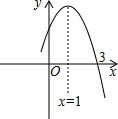 若y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的另一个解为( )
若y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的另一个解为( )| A、-2 | B、-1 | C、0 | D、1 |
 如图,△ABC中,点D在AB边上,∠A=∠1,∠B=∠2,则△ABC的形状是( )
如图,△ABC中,点D在AB边上,∠A=∠1,∠B=∠2,则△ABC的形状是( )| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
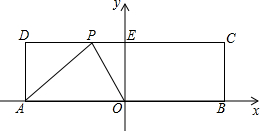 如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标.
如图所示,在平面直角坐标系中,O为原点,四边形ABCD是长方形且关于y轴对称,A(-5,0),B(5,0),C(5,3),点P在CD上运动,当△APO是腰长为5的等腰三角形时,求点P的坐标. 如图,点E在DF上,点B在AC上,BD∥CE,∠C=∠D,∠A与∠F相等吗?为什么?
如图,点E在DF上,点B在AC上,BD∥CE,∠C=∠D,∠A与∠F相等吗?为什么? 已知:如图,BD是△ABC的高,AB=6,AC=5
已知:如图,BD是△ABC的高,AB=6,AC=5