题目内容
7.等边三角形的边长为4,则它的面积是4$\sqrt{3}$.分析 根据等边三角形三线合一的性质可以求得高线AD的长度,根据BC和AD即可求得三角形的面积.
解答  解:如图,∵等边三角形三线合一,
解:如图,∵等边三角形三线合一,
∴D为BC的中点,BD=DC=2,
在Rt△ABD中,AB=4,BD=2,
∴AD=$\sqrt{{AB}^{2}{-BD}^{2}}$=2$\sqrt{3}$,
∴等边△ABC的面积为$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查了勾股定理在直角三角形中的运用,考查了三角形面积的计算,考查了等边三角形各边长相等的性质,本题中根据勾股定理即可AD的长度是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列计算正确的是( )
| A. | 3a-a=3 | B. | a2+a2=a4 | C. | (3a)-(2a)=6a | D. | (a2)3=a6 |
15.已知a、b满足a+b=5且ab=6,以a、b为根的一元二次方程为( )
| A. | x2+5x+6=0 | B. | x2-5x+6=0 | C. | x2-5x-6=0 | D. | x2+5x-6=0 |
2.已知x=1是关于x的一元二次方程x2-2ax+1=0的一个根,则a的值是( )
| A. | 1 | B. | 0 | C. | 2或-2 | D. | $\frac{1}{2}$ |
17.下列命题中,为真命题的是( )
| A. | 有一组邻边相等的四边形是菱形 | |
| B. | 有一个角是直角的平行四边形是矩形 | |
| C. | 有一组对边平行的四边形是平行四边形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
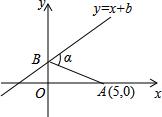 如图,已知A点坐标为(5,0),直线y=x+b与y轴交于点B,连接AB,α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.
如图,已知A点坐标为(5,0),直线y=x+b与y轴交于点B,连接AB,α=75°,则b的值为$\frac{5\sqrt{3}}{3}$. 如图,AB∥ED,∠B+∠C+∠D=360°.
如图,AB∥ED,∠B+∠C+∠D=360°. 如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,AB为⊙O的切线,且AB=AC.图中阴影部分的面积是$\frac{8}{3}$π+4$\sqrt{3}$.
如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,AB为⊙O的切线,且AB=AC.图中阴影部分的面积是$\frac{8}{3}$π+4$\sqrt{3}$. 如图,已知在长方形ABCD中,AB=10cm,BC=8cm,点E是CD中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E,若点P运动的时间为x秒,那么当x=4或6.6s时,△APE的面积等于32cm.
如图,已知在长方形ABCD中,AB=10cm,BC=8cm,点E是CD中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E,若点P运动的时间为x秒,那么当x=4或6.6s时,△APE的面积等于32cm.