题目内容
12．
如图，在?ABCD中，已知AD=6cm，AB=8cm，CE平分∠BCD交BC边于点E，则AE的长为（ ）| A． | 2cm | B． | 4cm | C． | 6cm | D． | 8cm |
分析 利用平行四边形的性质以及角平分线的性质得出∠BEC=∠BCE，进而得出BE=BC=6cm，再根据AE=AB-BE计算即可．
解答 解：∵在?ABCD中，AB∥CD，AB=CD=8cm，BC=AD=6cm，
∴∠DCE=∠BEC，
∵CE平分∠BCD，
∴∠DCE=∠BCE，
∴∠BEC=∠BCE，
∴BE=BC=6cm，
∴AE=AB-BE=2cm，
故选：A．
点评 此题主要考查了平行四边形的性质以及角平分线的性质，得出BE=BC是解题关键．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
3．
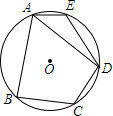如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=120°，点E在弧AD上．若AE恰好为⊙O的内接正十边形的一边，弧DE的度数为（ ）
如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=120°，点E在弧AD上．若AE恰好为⊙O的内接正十边形的一边，弧DE的度数为（ ）| A． | 75° | B． | 80° | C． | 84° | D． | 90° |
20．
如图，是二次函数y=ax2+bx+c图象的一部分，对称轴为直线x=-1，且过点（-4，0），给出四个结论：①abc＜0 ②2a-b=0 ③4a+2b+c＜0 ④若点（-6，y1），（3，y2）是该抛物线上的两点，则y1＞y2，其中正确的是（ ）
如图，是二次函数y=ax2+bx+c图象的一部分，对称轴为直线x=-1，且过点（-4，0），给出四个结论：①abc＜0 ②2a-b=0 ③4a+2b+c＜0 ④若点（-6，y1），（3，y2）是该抛物线上的两点，则y1＞y2，其中正确的是（ ）| A． | ①② | B． | ①②④ | C． | ②③ | D． | ②③④ |
7．已知△ABC中，AB=AC，AB的垂直平分线交AC于D，△ABC和△DBC的周长分别是70cm和48cm，则△ABC的腰和底边长分别为（ ）
| A． | 24cm和22cm | B． | 26cm和18cm | C． | 22cm和26cm | D． | 23cm和24cm |
4．下列运算正确的是（ ）
| A． | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B． | $\sqrt{4\frac{1}{9}}=2\frac{1}{3}$ | C． | $\sqrt{8}-\sqrt{2}=\sqrt{2}$ | D． | $\sqrt{8}÷\sqrt{2}=4$ |