题目内容
6.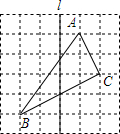 如图,每个小正方形的边长都是1.
如图,每个小正方形的边长都是1.(1)画出图中格点三角形ABC关于已知直线l对称的△A′B′C′,并求△A′B′C′的面积;
(2)判断△ABC的形状,并证明你的结论.
分析 (1)根据轴对称的性质画出△A′B′C′,利用矩形的面积减去三个顶点上三角形的面积即可;
(2)根据勾股定理的逆定理判断出△ABC的形状即可.
解答  解:(1)如图所示,S△A′B′C′=4×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×2×1-$\frac{1}{2}$×4×3
解:(1)如图所示,S△A′B′C′=4×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×2×1-$\frac{1}{2}$×4×3
=16-4-1-6
=5.
(2)△ABC是直角三角形.
∵AC2=12+22=5,BC2=42+22=20,AB2=32+42=25,
∴AC2+BC2=AB2,
∴∠ACB=90°即△ABC是直角三角形.
点评 本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
17.一个小球以15m/s的初速度竖直向上弹出,它在空中的高度的h(m)与时间t(s)满足关系:h=15t-5t2,小球何时能达到10m高?( )
| A. | 2s | B. | 1s | C. | 1s或2s | D. | 无法确定 |
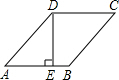 如图,在菱形ABCD中,DE⊥AB于E,DE=6,sinA=$\frac{4}{5}$,则菱形ABCD的面积是45.
如图,在菱形ABCD中,DE⊥AB于E,DE=6,sinA=$\frac{4}{5}$,则菱形ABCD的面积是45. 如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,PN+PM+MN的最小值是5cm,则∠AOB的度数是30°.
如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,PN+PM+MN的最小值是5cm,则∠AOB的度数是30°.

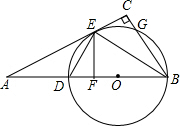 如图,在△ABC中,∠C=90°,BE是∠ABC的平分线,过点E作BE的垂线交AB于点F,⊙O是△BDE的外接圆.求证:
如图,在△ABC中,∠C=90°,BE是∠ABC的平分线,过点E作BE的垂线交AB于点F,⊙O是△BDE的外接圆.求证: