题目内容
1. 如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,PN+PM+MN的最小值是5cm,则∠AOB的度数是30°.
如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,PN+PM+MN的最小值是5cm,则∠AOB的度数是30°.
分析 分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,由对称的性质得出PM=CM,OP=OC,∠COA=∠POA;PN=DN,OP=OD,∠DOB=∠POB,得出∠AOB=$\frac{1}{2}$∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
解答 解:分别作点P关于OA、OB的对称点C、D,连接CD,
分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB=$\frac{1}{2}$∠COD,
∵PN+PM+MN的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°.
故答案为:30°.
点评 本题考查了轴对称的性质、最短路线问题、等边三角形的判定与性质;熟练掌握轴对称的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
12.某地一天的最高气温是12℃,最低气温是-2℃,则该地这天的温差是( )
| A. | -10℃ | B. | 10℃ | C. | 14℃ | D. | -14℃ |
9.下列计算中,正确的是( )
| A. | -2(a+b)=-2a+b | B. | -2(a+b)=-2a-b2 | C. | -2(a+b)=-2a-2b | D. | -2(a+b)=-2a+2b |
16.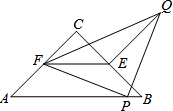 如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )
如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )
 如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )
如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
10.某制药厂生产的某种针剂,每支成本3元,由于连续两次降低成本,现在的成本是2.43元,则平均每次降低成本的百分率是( )
| A. | 10% | B. | 20% | C. | 7% | D. | 8% |
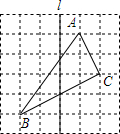 如图,每个小正方形的边长都是1.
如图,每个小正方形的边长都是1.