题目内容
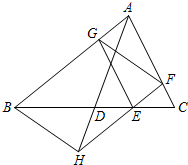 已知:如图,在△ABC中,AD是边BC上的中线,点E在线段DC上,EF∥AB交边AC于点F,EG∥AC交边AB于点G,FE的延长线与AD的延长线交于点H.
已知:如图,在△ABC中,AD是边BC上的中线,点E在线段DC上,EF∥AB交边AC于点F,EG∥AC交边AB于点G,FE的延长线与AD的延长线交于点H.求证:GF=BH.
考点:相似三角形的判定与性质,全等三角形的判定与性质
专题:证明题
分析:先延长AD至A′,使DA′=AD,连接A′B,A′C,得出A′C∥AB,A′C=AB,再证出HF∥A′C,得出
=
,再根据平行线分线段成比例定理得出
=
,HF∥BG且GF=BH,从而证出四边形BGFH为平行四边形,即可得出答案.
| HF |
| A′C |
| AF |
| AC |
| EG |
| A′C |
| BH |
| BA |
解答:证明:延长AD至A′,使DA′=AD,连接A′B,A′C,
∵BD=CD,
∴四边形ABA′C为平行四边形,
∴A′C∥AB,A′C=AB,
∵HF∥A′C,
∴
=
,
又∵HF∥AB,EG∥AC,
∴
=
,
=
,
∴
=
,
∵A′C=AB,
∴HF=BG,
∴BG∥HF且BG=HF,
∴四边形BGFH为平行四边形,
∴GF=BH.

∵BD=CD,
∴四边形ABA′C为平行四边形,
∴A′C∥AB,A′C=AB,
∵HF∥A′C,
∴
| HF |
| A′C |
| AF |
| AC |
又∵HF∥AB,EG∥AC,
∴
| AF |
| AC |
| BE |
| BC |
| BE |
| BC |
| BG |
| AB |
∴
| HF |
| A′C |
| BG |
| AB |
∵A′C=AB,
∴HF=BG,
∴BG∥HF且BG=HF,
∴四边形BGFH为平行四边形,
∴GF=BH.
点评:点评:此题考查了平行线分线段成比例定理,用到的知识点是平行线分线段成比例定理,平行四边形的判定与性质,关键是根据题意作出辅助线,构造平行四边形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
据《纽约时报》报道,失踪的MH370客机根据雷达数据显示高度突变、两次改变航道.客机飞至13700多米(超限)高度后突然向西转,后不平稳降至7000多米,转向印度洋后,飞至较高海拔.13700用科学记数法表示是( )
| A、0.137×105 |
| B、13.7×103 |
| C、1.37×104 |
| D、137×102 |
 如图,在△ABC中,AB=2
如图,在△ABC中,AB=2 如图,在平面直角坐标系xOy中,两反比例函数y=
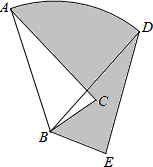
如图,在平面直角坐标系xOy中,两反比例函数y= 已知:如图,AB是半圆O的直径,CD⊥AB于D点,AD=4cm,DB=8cm,求BC的长.
已知:如图,AB是半圆O的直径,CD⊥AB于D点,AD=4cm,DB=8cm,求BC的长.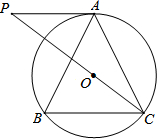 如图,⊙O是△ABC的外接圆,AB=AC,连结CO并延长交⊙O的切线AP于点P.
如图,⊙O是△ABC的外接圆,AB=AC,连结CO并延长交⊙O的切线AP于点P.