题目内容
在一个不透明的口袋里装有分别标有数字1，2，3，4四个小球，除数字不同外，小球没有任何区别．若从中随机取两个球，请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率．
考点：列表法与树状图法
专题：计算题
分析：列表得出所有等可能的情况数，找出两个球上的数字之和为偶数的情况即可求出所求的概率．
解答：解：列表如下：
所有等可能的情况有12种，其中两个球上的数字之和为偶数的情况有4种，
则P=
=
．
| 1 | 2 | 3 | 4 | |
| 1 | --- | （2，1） | （3，1） | （4，1） |
| 2 | （1，2） | --- | （3，2） | （4，2） |
| 3 | （1，3） | （2，3） | --- | （4，3） |
| 4 | （1，4） | （2，4） | （3，4） | --- |
则P=
| 4 |
| 12 |
| 1 |
| 3 |
点评：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
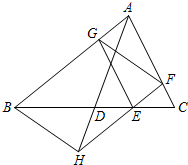已知：如图，在△ABC中，AD是边BC上的中线，点E在线段DC上，EF∥AB交边AC于点F，EG∥AC交边AB于点G，FE的延长线与AD的延长线交于点H．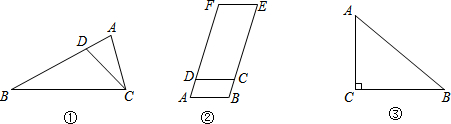
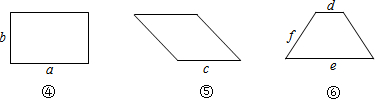
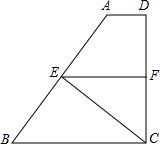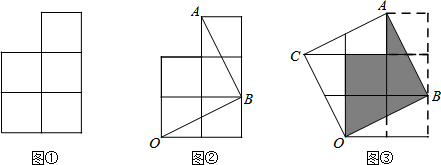
梯形ABCD中，AD∥BC，DC⊥BC，CE⊥AB于点E，点F在边CD上，且BE•CE=BC•CF．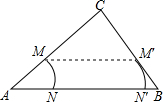
如图，Rt△ABC中，∠C=90°，BC=3，AC=4，M为边AC上一点（不包括点A和C），以点A为圆心，AM长为半径作劣弧交AB于点N，将
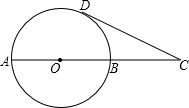如图，在⊙O中，过直径AB延长线上的点C作⊙O的一条切线，切点于D，若AC=10，AB=6，则sinC的值为