Question

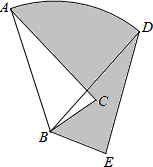如图，在△ABC中，AB=2

3

，将△ABC绕点B顺时针旋转60°后得到△DBE，点A经过的路径为弧AD，则图中阴影部分的面积是

 

．

Answer 1

考点：扇形面积的计算

专题：

分析：图中阴影部分的面积=扇形ABD的面积+三角形DBE的面积-三角形ABC的面积．又由旋转的性质知△ABC≌△DBE，所以三角形DBE的面积=三角形ABC的面积．

解答：解：∵根据旋转的性质知∠ABD=60°，△ABC≌△DBE，
∴S_△ABC-S_△DBE，
∴S_阴影=S_扇形ABD+S_△DBE-S_△ABC=S_扇形ABD=

60π×(2 3 )2

360

=2π．
故答案是：2π．

点评：本题考查了扇形面积的计算．解题的难点是找出图中阴影部分的面积=扇形ABD的面积+三角形DBE的面积-三角形ABC的面积．